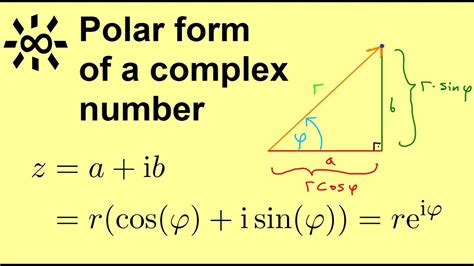In the realm of mathematics, complex numbers are a fundamental concept that extends the real number system to the complex plane. They are widely used in various fields, including algebra, geometry, trigonometry, and calculus. One of the essential tools for working with complex numbers is the polar form converter, which allows us to represent complex numbers in a more convenient and intuitive way.
What is the Polar Form of a Complex Number?

A complex number can be represented in two ways: rectangular (or Cartesian) form and polar form. The rectangular form expresses a complex number as a sum of a real part and an imaginary part, denoted by a + bi, where a and b are real numbers and i is the imaginary unit, which is defined as the square root of -1.
On the other hand, the polar form of a complex number represents it in terms of its magnitude (or length) and direction (or angle). This form is more intuitive and convenient for calculations involving complex numbers. The polar form of a complex number is denoted by r(cosθ + isinθ), where r is the magnitude (or length) of the complex number, θ is the angle (or argument) of the complex number, and i is the imaginary unit.
Benefits of Polar Form Converter

The polar form converter offers several benefits when working with complex numbers:
• Simplifies calculations: Polar form makes it easier to perform calculations involving complex numbers, such as multiplication and division. • Intuitive representation: The polar form provides a more intuitive representation of complex numbers, allowing for a better understanding of their properties and behavior. • Reduced errors: Using the polar form can reduce errors in calculations, as it eliminates the need to deal with complex fractions and algebraic manipulations. • Improved visualization: The polar form enables us to visualize complex numbers in a more meaningful way, making it easier to understand their geometric properties.
How to Convert Complex Numbers to Polar Form

To convert a complex number from rectangular form to polar form, follow these steps:
- Calculate the magnitude: Calculate the magnitude (or length) of the complex number using the formula r = √(a^2 + b^2), where a and b are the real and imaginary parts of the complex number, respectively.
- Calculate the angle: Calculate the angle (or argument) of the complex number using the formula θ = arctan(b/a), where a and b are the real and imaginary parts of the complex number, respectively.
- Write in polar form: Write the complex number in polar form using the formula r(cosθ + isinθ).
Practical Applications of Polar Form Converter

The polar form converter has numerous practical applications in various fields, including:
• Electrical engineering: Polar form is used to analyze and design AC circuits, filters, and transmission lines. • Signal processing: Polar form is used in signal processing techniques, such as Fourier analysis and modulation. • Navigation: Polar form is used in navigation systems, such as GPS, to calculate distances and angles between locations. • Computer graphics: Polar form is used in computer graphics to perform transformations and rotations of objects.
Common Challenges and Solutions

Some common challenges when working with polar form converters include:
• Difficulty in calculating magnitude and angle: To overcome this, use online calculators or software tools that can perform the calculations automatically. • Confusion between polar and rectangular forms: To avoid this, ensure that you understand the differences between the two forms and use the correct notation. • Difficulty in visualizing complex numbers: To overcome this, use graphical representations and plotting tools to visualize complex numbers in polar form.
Best Practices for Using Polar Form Converter

To get the most out of the polar form converter, follow these best practices:
• Use online calculators and software tools: Utilize online calculators and software tools to perform calculations and conversions quickly and accurately. • Understand the notation: Ensure that you understand the notation and conventions used in polar form. • Visualize complex numbers: Use graphical representations and plotting tools to visualize complex numbers in polar form.
In conclusion, the polar form converter is a powerful tool for simplifying complex numbers and performing calculations involving them. By understanding the benefits, applications, and challenges of polar form converters, you can harness their power to improve your mathematical skills and solve complex problems with ease.
What is the polar form of a complex number?
+The polar form of a complex number is a representation of the complex number in terms of its magnitude (or length) and direction (or angle). It is denoted by r(cosθ + isinθ), where r is the magnitude of the complex number, θ is the angle of the complex number, and i is the imaginary unit.
How do I convert a complex number from rectangular form to polar form?
+To convert a complex number from rectangular form to polar form, calculate the magnitude (or length) of the complex number using the formula r = √(a^2 + b^2), where a and b are the real and imaginary parts of the complex number, respectively. Then, calculate the angle (or argument) of the complex number using the formula θ = arctan(b/a). Finally, write the complex number in polar form using the formula r(cosθ + isinθ).
What are some common challenges when working with polar form converters?
+Some common challenges when working with polar form converters include difficulty in calculating magnitude and angle, confusion between polar and rectangular forms, and difficulty in visualizing complex numbers. To overcome these challenges, use online calculators and software tools, ensure that you understand the notation and conventions used in polar form, and use graphical representations and plotting tools to visualize complex numbers in polar form.