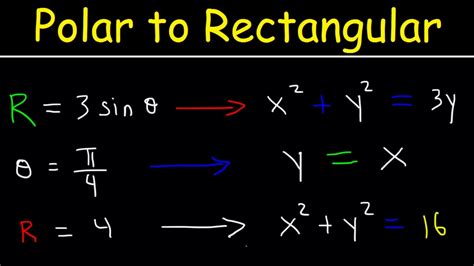Convert Polar Equations To Rectangular Form Easily

Quick Links :

Converting polar equations to rectangular form is a crucial skill in mathematics, particularly in calculus, algebra, and geometry. It allows us to transform equations that are given in terms of polar coordinates, which involve the radius and angle of a point, into equations that are expressed in terms of x and y, the rectangular coordinates. This conversion is essential for solving equations, graphing curves, and understanding the properties of various shapes.

The ability to convert between polar and rectangular coordinates provides a powerful tool for problem-solving in various fields, including physics, engineering, and computer science. By mastering this conversion, students and professionals can tackle complex problems with ease and accuracy.

Understanding Polar Coordinates

Before we dive into the conversion process, let's review the basics of polar coordinates. In a polar coordinate system, a point is represented by its distance from the origin (r) and the angle it makes with the positive x-axis (θ). The rectangular coordinates (x, y) can be expressed in terms of polar coordinates using the following equations:

x = r cos θ y = r sin θ

These equations form the foundation of converting polar equations to rectangular form.

Conversion Techniques

There are several techniques to convert polar equations to rectangular form. Here are some common methods:

Method 1: Using Trigonometric Identities

One way to convert polar equations is to use trigonometric identities to express the equation in terms of x and y. For example, consider the polar equation:

r = 2 sin θ

We can use the trigonometric identity sin θ = y/r to rewrite the equation as:

r = 2y/r

Multiplying both sides by r, we get:

r^2 = 2y

Substituting x = r cos θ and y = r sin θ, we can rewrite the equation as:

x^2 + y^2 = 2y

This is the rectangular form of the polar equation.

Method 2: Using the Double-Angle Formula

Another method is to use the double-angle formula to convert polar equations. For example, consider the polar equation:

r = 2 cos 2θ

We can use the double-angle formula cos 2θ = 1 - 2 sin^2 θ to rewrite the equation as:

r = 2 (1 - 2 sin^2 θ)

Substituting x = r cos θ and y = r sin θ, we can rewrite the equation as:

x^2 + y^2 = 2x^2 - 4y^2

This is the rectangular form of the polar equation.

Method 3: Using the Half-Angle Formula

A third method is to use the half-angle formula to convert polar equations. For example, consider the polar equation:

r = 2 sin (θ/2)

We can use the half-angle formula sin (θ/2) = ±√((1 - cos θ)/2) to rewrite the equation as:

r = ±2√((1 - cos θ)/2)

Substituting x = r cos θ and y = r sin θ, we can rewrite the equation as:

x^2 + y^2 = 4 (1 - x^2/r^2)

This is the rectangular form of the polar equation.

Applications of Converting Polar Equations

Converting polar equations to rectangular form has numerous applications in mathematics, physics, and engineering. Here are some examples:

Graphing Curves

Converting polar equations to rectangular form allows us to graph curves that are difficult to visualize in polar coordinates. For example, the polar equation:

r = 2 sin θ

can be converted to the rectangular equation:

x^2 + y^2 = 2y

This equation represents a circle with center (0, 1) and radius 1.

Solving Equations

Converting polar equations to rectangular form can also help us solve equations that are difficult to solve in polar coordinates. For example, consider the polar equation:

r = 2 cos θ + 3 sin θ

We can convert this equation to the rectangular equation:

x^2 + y^2 = 2x + 3y

This equation represents a conic section, and we can solve it using standard techniques.

Conclusion: Mastering the Art of Conversion

Converting polar equations to rectangular form is an essential skill in mathematics and physics. By mastering this conversion, we can tackle complex problems with ease and accuracy. Whether we're graphing curves, solving equations, or modeling real-world phenomena, the ability to convert between polar and rectangular coordinates is a powerful tool that can help us achieve our goals.