Point Slope Form Math Definition Made Easy

Quick Links :

Mathematics is an integral part of our daily lives, and understanding its various concepts can help us solve problems and make informed decisions. One such concept is the point-slope form, which is a fundamental idea in algebra and geometry. In this article, we will delve into the world of point-slope form, explore its definition, and provide examples to help you understand this concept better.

Point-slope form is a way of representing a linear equation in mathematics. It is a powerful tool that helps us find the equation of a line when we know the slope and a point on the line. The point-slope form is particularly useful when we are dealing with word problems or real-world applications, where we need to find the equation of a line that passes through a specific point.

What is Point-Slope Form?

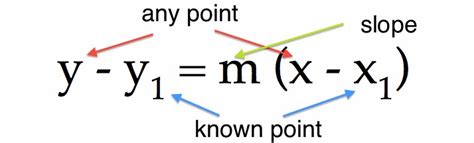
The point-slope form is a linear equation that represents a line on a coordinate plane. It is written in the form:

y - y1 = m(x - x1)

where (x1, y1) is a point on the line, and m is the slope of the line. The slope is a measure of how steep the line is, and it can be positive, negative, or zero.

Understanding the Components of Point-Slope Form

To understand the point-slope form, let's break down its components:

• (x1, y1) is a point on the line. This point can be any point on the line, but it's usually the point that is given in the problem.
• m is the slope of the line. The slope can be calculated using the formula:

m = (y2 - y1) / (x2 - x1)

where (x2, y2) is another point on the line.

• y - y1 is the change in y-coordinates. This represents the vertical distance between the point (x1, y1) and the point (x, y).
• m(x - x1) is the change in x-coordinates multiplied by the slope. This represents the horizontal distance between the point (x1, y1) and the point (x, y).

How to Use Point-Slope Form

Using the point-slope form is a straightforward process. Here are the steps:

1. Identify the point on the line. This can be any point on the line, but it's usually the point that is given in the problem.
2. Find the slope of the line. This can be done using the formula:

m = (y2 - y1) / (x2 - x1)

3. Plug the values into the point-slope form equation:

y - y1 = m(x - x1)

4. Simplify the equation, if necessary.

Examples of Point-Slope Form

Let's look at some examples to illustrate how to use the point-slope form:

Example 1: Find the equation of the line that passes through the point (2, 3) and has a slope of 2.

Solution:

y - 3 = 2(x - 2)

Simplifying the equation, we get:

y = 2x - 1

Example 2: Find the equation of the line that passes through the points (1, 2) and (3, 4).

Solution:

First, we need to find the slope of the line. Using the formula, we get:

m = (4 - 2) / (3 - 1) = 2 / 2 = 1

Next, we can use either point to write the equation of the line. Let's use the point (1, 2).

y - 2 = 1(x - 1)

Simplifying the equation, we get:

y = x + 1

Benefits of Using Point-Slope Form

There are several benefits of using the point-slope form:

• It is a powerful tool for finding the equation of a line when we know the slope and a point on the line.
• It is useful for solving word problems and real-world applications, where we need to find the equation of a line that passes through a specific point.
• It is a flexible equation that can be used to find the equation of a line in different forms, such as slope-intercept form or standard form.

Common Mistakes to Avoid

When using the point-slope form, there are several common mistakes to avoid:

• Make sure to plug in the correct values for the point and slope.
• Simplify the equation, if necessary, to get the final answer.
• Check your work by graphing the line or using another method to verify the equation.

We hope this article has helped you understand the point-slope form and how to use it to find the equation of a line. With practice and patience, you can become proficient in using this powerful tool to solve problems and make informed decisions.

Now it's your turn! Share your thoughts and experiences with the point-slope form in the comments below. Do you have any questions or need further clarification? Share this article with your friends and colleagues who may benefit from it.