Exploring Point Slope Form: A Fun Math Activity

Quick Links :

Mathematics, often viewed as a dry and complex subject, holds within it a world of excitement and creativity waiting to be unleashed. Among the many fascinating aspects of math, the point slope form is a fundamental concept that not only simplifies understanding but also opens doors to a plethora of problem-solving opportunities. In this article, we'll embark on an exciting journey to explore the point slope form, its significance, and how it can make math a more engaging and enjoyable subject.

What is Point Slope Form?

At its core, the point slope form is a way to express the equation of a line. It is one of the three primary forms used to write linear equations, the other two being the slope-intercept form and the standard form. The point slope form is particularly useful when the slope of the line and a point it passes through are known.

Equation of Point Slope Form

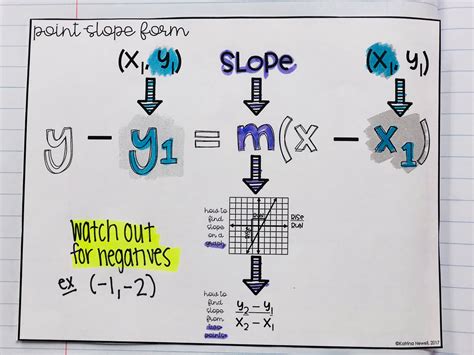
The equation of a line in point slope form is given by:

[y - y_1 = m(x - x_1)]

where:

• (m) is the slope of the line.
• ((x_1, y_1)) is the point the line passes through.

This equation encapsulates the essence of the line, conveying both its steepness (slope) and a specific point through which it passes.

Why is Point Slope Form Important?

The point slope form is a versatile tool in mathematics and real-world applications. It allows for the calculation of slopes and equations of lines when a point and the slope are known. This form is particularly useful in coordinate geometry, calculus, and physics, among other disciplines.

Real-World Applications

1. Physics and Engineering: The point slope form can be used to describe the motion of objects, including the path of projectiles and the stress on materials in buildings and bridges.
2. Computer Graphics: This form is crucial in rendering 2D and 3D images, helping to create the illusion of depth on a flat screen.
3. Economics: The point slope form can model supply and demand curves, helping economists understand how prices and quantities of goods and services interact.

How to Use Point Slope Form

Using the point slope form involves understanding its components and applying them to given problems. Here's a step-by-step guide:

1. Identify the Slope (m): The slope is a measure of how steep the line is. It can be positive, negative, zero, or undefined.
2. Identify the Point (x1, y1): This is any point that the line passes through.
3. Apply the Formula: Plug the slope and the point into the equation (y - y_1 = m(x - x_1)) to get the equation of the line.
4. Simplify (if necessary): Depending on the problem, you might need to simplify the equation to make it more usable.

Practical Example

Given that a line has a slope of 2 and passes through the point (3, 4), what is its equation?

[y - 4 = 2(x - 3)]

[y - 4 = 2x - 6]

[y = 2x - 2]

Making Math Fun with Point Slope Form

Math can indeed be fun, especially when you're creating and exploring your own equations using the point slope form. Here are some ideas to get you started:

1. Graphical Exploration: Use graphing software or apps to visualize lines created from different slopes and points.
2. Creative Problems: Invent real-world scenarios (e.g., designing a skateboard ramp, planning a garden path) that require the use of point slope form to solve.
3. Math Games: Develop simple games where players have to identify slopes or points to draw lines correctly.

Conclusion - The Joy of Math Discovery

The point slope form is more than just a mathematical concept; it's a gateway to exploring the beauty and utility of mathematics. By engaging with it, not only do we learn how to express linear equations in a useful form, but we also tap into the creativity and problem-solving aspects of math that make it so compelling.

We hope this journey through the point slope form has inspired you to see mathematics in a new light, as a subject that combines logic, creativity, and fun. Whether you're a student, teacher, or simply a curious individual, the point slope form offers a fascinating world of discovery and application.

Now, take the next step in your math adventure. Try creating your own equations using the point slope form, explore how it's used in different subjects, or invent games and challenges that incorporate this concept. The joy of math discovery awaits!