Newtons Second Law In Component Form Explained

Quick Links :

Understanding the intricacies of physics can be a daunting task, but Newton's Second Law is a fundamental concept that has far-reaching implications in various fields. This law, also known as the law of acceleration, helps us understand how forces affect the motion of objects. In this article, we will delve into Newton's Second Law in component form, exploring its significance, mathematical representations, and practical applications.

What is Newton's Second Law?

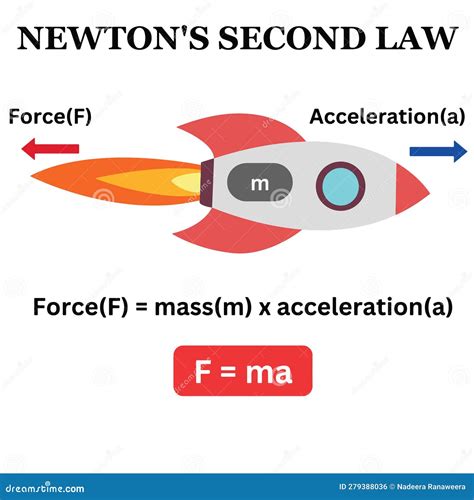
Newton's Second Law states that the acceleration of an object is directly proportional to the net force acting upon it and inversely proportional to its mass. Mathematically, this is represented as F = ma, where F is the net force applied to the object, m is its mass, and a is the resulting acceleration.

Newton's Second Law in Component Form

When dealing with complex systems or objects moving in multiple directions, it's essential to break down the forces and accelerations into their component parts. This is where Newton's Second Law in component form comes into play.

In two-dimensional motion, we can resolve the forces and accelerations into x and y components. This allows us to analyze the motion of objects in a more detailed and accurate manner. For instance, consider a car moving around a curve on a horizontal surface. We can resolve the force of friction into its x and y components to understand the car's acceleration and motion.

In three-dimensional motion, we need to consider the x, y, and z components of the forces and accelerations. This is particularly important in fields like aerospace engineering, where objects are moving in complex trajectories.

Mathematical Representation

The mathematical representation of Newton's Second Law in component form is as follows:

Fx = max Fy = may Fz = maz

where Fx, Fy, and Fz are the x, y, and z components of the net force, and ax, ay, and az are the corresponding components of the acceleration.

Practical Applications

Understanding Newton's Second Law in component form has numerous practical applications in various fields, including:

• Aerospace engineering: Analyzing the motion of aircraft and spacecraft requires breaking down the forces and accelerations into their component parts.
• Automotive engineering: Designing vehicles that can maneuver safely and efficiently relies on understanding the component forces and accelerations.
• Robotics: Accurate motion control and navigation in robots depend on applying Newton's Second Law in component form.

Real-World Examples

1. Projectile Motion: When throwing a ball or launching a rocket, we need to consider the component forces and accelerations to predict the trajectory and range.
2. Car Safety: Designing airbags and safety features requires understanding the component forces and accelerations during a crash.
3. Robotics: Controlling the motion of robots in manufacturing and healthcare relies on applying Newton's Second Law in component form.

Benefits of Understanding Newton's Second Law in Component Form

Understanding Newton's Second Law in component form offers several benefits, including:

• Improved accuracy in predicting motion and behavior
• Enhanced design and analysis of complex systems
• Better decision-making in fields like aerospace and automotive engineering
• Increased efficiency and safety in robotics and manufacturing

Challenges and Limitations

While understanding Newton's Second Law in component form is essential, there are challenges and limitations to consider, such as:

• Complexity: Breaking down forces and accelerations into their component parts can be mathematically intensive.
• Assumptions: Simplifying assumptions may be necessary to analyze complex systems.
• Real-world variations: Actual systems may exhibit variations and uncertainties that affect the accuracy of calculations.

Conclusion

Newton's Second Law in component form is a fundamental concept in physics that has far-reaching implications in various fields. By understanding the mathematical representation and practical applications, we can improve our analysis and design of complex systems. While there are challenges and limitations to consider, the benefits of understanding Newton's Second Law in component form make it an essential tool in the field of physics.

We hope this article has provided a comprehensive overview of Newton's Second Law in component form. Share your thoughts and questions in the comments below!