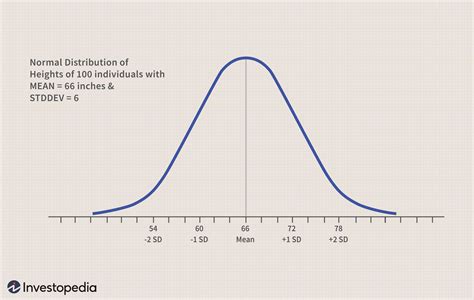
The normal distribution, also known as the Gaussian distribution or bell curve, is a fundamental concept in statistics and data analysis. It is a probability distribution that is commonly observed in natural phenomena, such as the distribution of heights, weights, and IQ scores. Understanding the normal distribution is crucial for making informed decisions in various fields, including business, economics, medicine, and social sciences.
The normal distribution is widely used because it provides a simple and effective way to model and analyze complex data. It is characterized by its symmetrical shape, with the majority of the data points clustered around the mean and tapering off gradually towards the extremes. This distribution is essential for statistical inference, hypothesis testing, and confidence intervals. In this article, we will explore the normal distribution in five essential points, providing a comprehensive understanding of this fundamental concept.
What is the Normal Distribution?

The normal distribution is a probability distribution that is defined by the following characteristics:
- It is symmetrical around the mean, which is the average value of the data.
- It is bell-shaped, with the majority of the data points clustered around the mean.
- It is continuous, meaning that the data can take on any value within a given range.
- It is unimodal, meaning that it has a single peak.
The normal distribution is often represented by the following probability density function:
f(x) = (1/√(2πσ^2)) * e^(-(x-μ)^2 / (2σ^2))
where x is the data value, μ is the mean, σ is the standard deviation, and e is the base of the natural logarithm.
Properties of the Normal Distribution

The normal distribution has several important properties that make it useful for statistical analysis:
- Symmetry: The normal distribution is symmetrical around the mean, which means that the data is evenly distributed on both sides of the mean.
- Unimodality: The normal distribution has a single peak, which means that there is only one mode.
- Continuity: The normal distribution is continuous, meaning that the data can take on any value within a given range.
- Independence: The normal distribution is independent of the data's origin, which means that the distribution of the data does not depend on the starting point.
These properties make the normal distribution a powerful tool for statistical analysis and modeling.
Why is the Normal Distribution Important?
The normal distribution is essential for statistical inference, hypothesis testing, and confidence intervals. It is widely used in various fields, including business, economics, medicine, and social sciences. Here are some reasons why the normal distribution is important:
- Modeling: The normal distribution is used to model complex data and make predictions about future outcomes.
- Hypothesis testing: The normal distribution is used to test hypotheses about population parameters, such as the mean and standard deviation.
- Confidence intervals: The normal distribution is used to construct confidence intervals, which provide a range of values within which a population parameter is likely to lie.
Applications of the Normal Distribution

The normal distribution has numerous applications in various fields, including:
- Finance: The normal distribution is used to model stock prices, returns, and risk.
- Medicine: The normal distribution is used to model the distribution of health outcomes, such as blood pressure and cholesterol levels.
- Social sciences: The normal distribution is used to model the distribution of social phenomena, such as IQ scores and personality traits.
These applications demonstrate the importance of the normal distribution in understanding and analyzing complex data.
Common Mistakes to Avoid
When working with the normal distribution, there are several common mistakes to avoid:
- Assuming normality: Do not assume that a dataset follows a normal distribution without checking the data's distribution.
- Ignoring outliers: Do not ignore outliers, as they can affect the accuracy of the results.
- Using the wrong parameters: Do not use the wrong parameters, such as the mean and standard deviation, when working with the normal distribution.
By avoiding these common mistakes, you can ensure accurate and reliable results when working with the normal distribution.
Conclusion

In conclusion, the normal distribution is a fundamental concept in statistics and data analysis. It is widely used in various fields, including business, economics, medicine, and social sciences. By understanding the normal distribution, you can make informed decisions and analyze complex data with confidence.
We hope that this article has provided a comprehensive understanding of the normal distribution and its applications. If you have any questions or comments, please feel free to share them below.
What is the normal distribution?
+The normal distribution is a probability distribution that is defined by its symmetrical shape, with the majority of the data points clustered around the mean and tapering off gradually towards the extremes.
Why is the normal distribution important?
+The normal distribution is essential for statistical inference, hypothesis testing, and confidence intervals. It is widely used in various fields, including business, economics, medicine, and social sciences.
What are the properties of the normal distribution?
+The normal distribution has several important properties, including symmetry, unimodality, continuity, and independence.