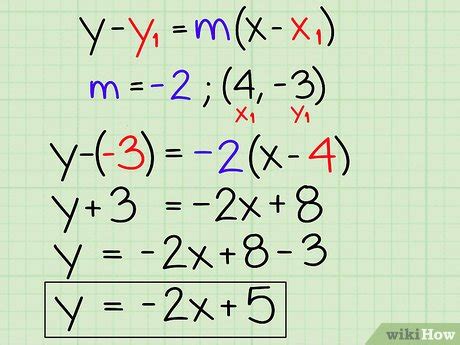Write Slope Intercept Form In 5 Easy Steps

Quick Links :

Slope-intercept form is a fundamental concept in algebra and a crucial skill for solving linear equations. Mastering this form can make a significant difference in your math journey, especially when dealing with graphing lines, solving systems of equations, and modeling real-world problems. In this article, we'll break down the slope-intercept form into 5 easy steps, making it accessible to students of all levels.

Understanding Slope-Intercept Form

Slope-intercept form, denoted as y = mx + b, is a way to express a linear equation in a graphical format. The equation consists of two main components: the slope (m) and the y-intercept (b). The slope represents the rate of change between the x and y variables, while the y-intercept is the point at which the line crosses the y-axis.

Why is Slope-Intercept Form Important?

Slope-intercept form is essential in various mathematical and real-world applications, including:

• Graphing lines: By knowing the slope and y-intercept, you can easily graph a line on a coordinate plane.
• Solving systems of equations: Slope-intercept form makes it easier to solve systems of linear equations by allowing you to quickly identify the intersection point.
• Modeling real-world problems: Many real-world problems, such as population growth, financial transactions, and physics, can be modeled using linear equations in slope-intercept form.

Step 1: Identify the Slope (m)

The slope (m) is a measure of how steep a line is. It's calculated by dividing the change in y-coordinates (rise) by the change in x-coordinates (run). The formula for slope is:

m = (y2 - y1) / (x2 - x1)

To find the slope, you can use two points on the line or the coefficient of x in the equation.

Example: Find the Slope

Find the slope of the line passing through points (2, 3) and (4, 5).

m = (5 - 3) / (4 - 2) m = 2 / 2 m = 1

Step 2: Find the Y-Intercept (b)

The y-intercept (b) is the point at which the line crosses the y-axis. To find the y-intercept, you can use one of the following methods:

• Use the slope-intercept form equation: y = mx + b, where m is the slope and b is the y-intercept.
• Find the point on the line where x = 0.

Example: Find the Y-Intercept

Find the y-intercept of the line with slope m = 1 and passing through point (2, 3).

3 = 1(2) + b 3 = 2 + b b = 1

Step 3: Write the Equation in Slope-Intercept Form

Now that you have the slope (m) and y-intercept (b), you can write the equation in slope-intercept form:

y = mx + b

Example: Write the Equation

Write the equation of the line with slope m = 1 and y-intercept b = 1.

y = 1x + 1 y = x + 1

Step 4: Graph the Line (Optional)

If you want to visualize the line, you can graph it on a coordinate plane using the slope-intercept form equation.

Example: Graph the Line

Graph the line y = x + 1.

To graph the line, plot the y-intercept (0, 1) and use the slope (1) to find another point on the line.

Step 5: Verify the Equation

To ensure that your equation is correct, you can plug in a point on the line and verify that it satisfies the equation.

Example: Verify the Equation

Verify that the point (2, 3) satisfies the equation y = x + 1.

3 = 2 + 1 3 = 3

The equation is correct!

By following these 5 easy steps, you can master the slope-intercept form and solve linear equations with confidence. Remember to practice, practice, practice to become proficient in this fundamental concept.

We'd love to hear from you! Share your thoughts, questions, or examples in the comments below. Don't forget to like and share this article with your friends and classmates.