Writing Expanded Form For Decimals Made Easy

Quick Links :

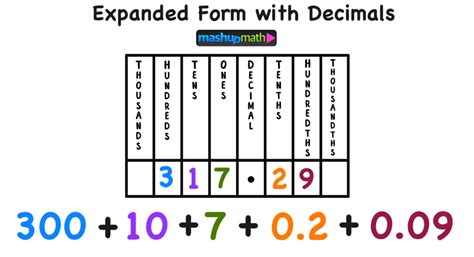
When it comes to decimals, one of the most fundamental concepts is writing them in expanded form. Expanded form, also known as expanded notation, is a way of expressing a number as a sum of its place values. This concept is essential for understanding more complex math concepts, such as fractions, percentages, and algebra. In this article, we will explore the concept of expanded form for decimals, its importance, and provide a step-by-step guide on how to write decimals in expanded form.

What is Expanded Form?

Expanded form is a way of expressing a number as a sum of its place values. It involves breaking down a number into its individual digits and multiplying each digit by its corresponding place value. For whole numbers, the place values are powers of 10 (1, 10, 100, 1000, etc.), while for decimals, the place values are powers of 10 divided by 10 (0.1, 0.01, 0.001, etc.).

Why is Expanded Form Important?

Expanded form is essential for understanding more complex math concepts, such as fractions, percentages, and algebra. It helps students visualize the relationships between digits and place values, making it easier to perform calculations and understand mathematical concepts. Additionally, expanded form is used in real-world applications, such as finance, science, and engineering, where accurate calculations are crucial.

Writing Decimals in Expanded Form

Writing decimals in expanded form involves breaking down the decimal into its individual digits and multiplying each digit by its corresponding place value. Here's a step-by-step guide:

1. Write the decimal number.
2. Identify the place value of each digit (0.1, 0.01, 0.001, etc.).
3. Multiply each digit by its corresponding place value.
4. Add the products together to get the expanded form.

Example: Write 4.27 in expanded form.

1. Write the decimal number: 4.27
2. Identify the place value of each digit: 4 (ones), 2 (tenths), 7 (hundredths)
3. Multiply each digit by its corresponding place value: 4 x 1 = 4, 2 x 0.1 = 0.2, 7 x 0.01 = 0.07
4. Add the products together: 4 + 0.2 + 0.07 = 4.27

Expanded form: 4 + 0.2 + 0.07

Practical Examples

Let's try a few more examples:

• Write 2.94 in expanded form: 2 + 0.9 + 0.04
• Write 1.18 in expanded form: 1 + 0.1 + 0.08
• Write 3.75 in expanded form: 3 + 0.7 + 0.05

Benefits of Writing Decimals in Expanded Form

Writing decimals in expanded form has several benefits:

• Improves understanding of place value
• Enhances calculation skills
• Develops problem-solving strategies
• Prepares students for more complex math concepts

Conclusion

In conclusion, writing decimals in expanded form is an essential math concept that helps students understand the relationships between digits and place values. By following the step-by-step guide and practicing with examples, students can master this concept and develop a stronger foundation in math.

Call to Action

We hope this article has helped you understand the concept of expanded form for decimals. Try practicing with more examples and share your experiences with us in the comments below! If you have any questions or need further clarification, feel free to ask.