Write A Quadratic In Standard Form: A Step-By-Step Guide

Quick Links :

Quadratic equations are a fundamental concept in algebra, and writing them in standard form is an essential skill for any math student. In this article, we will explore the importance of quadratic equations, their standard form, and provide a step-by-step guide on how to write a quadratic in standard form.

Quadratic equations are polynomial equations of degree two, which means the highest power of the variable (usually x) is two. They have numerous applications in various fields, including physics, engineering, economics, and computer science. Quadratic equations can be used to model real-world situations, such as the trajectory of a projectile, the design of electronic circuits, and the optimization of business processes.

What is Standard Form?

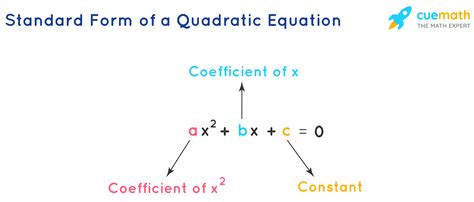
Standard form is a way of expressing a quadratic equation in a specific format, which makes it easier to analyze and solve. The standard form of a quadratic equation is:

ax^2 + bx + c = 0

where:

• a is the coefficient of the squared term (x^2)
• b is the coefficient of the linear term (x)
• c is the constant term

Why is Standard Form Important?

Writing a quadratic equation in standard form is crucial for several reasons:

1. Simplifies the equation: Standard form makes the equation easier to read and understand.
2. Facilitates solving: Standard form provides a clear structure for solving the equation using various methods, such as factoring, quadratic formula, or graphing.
3. Enables comparisons: Standard form allows for easy comparisons between different quadratic equations.

A Step-By-Step Guide to Writing a Quadratic in Standard Form

Now that we understand the importance of standard form, let's dive into the step-by-step process of writing a quadratic in standard form.

Step 1: Identify the Quadratic Equation

Start by identifying the quadratic equation you want to write in standard form. This can be a simple quadratic equation, such as x^2 + 5x + 6, or a more complex one, like 2x^2 - 3x - 1.

Step 2: Rearrange the Terms

Rearrange the terms of the quadratic equation to ensure the squared term (x^2) comes first, followed by the linear term (x), and finally the constant term.

Example:

2x^2 - 3x - 1 → 2x^2 + (-3x) + (-1)

Step 3: Combine Like Terms

Combine like terms, if any, to simplify the equation.

Example:

x^2 + 2x + 3x + 4 → x^2 + 5x + 4

Step 4: Write in Standard Form

Write the quadratic equation in standard form by ensuring the coefficients of the squared, linear, and constant terms are in the correct order.

Example:

x^2 + 5x + 4 → ax^2 + bx + c = x^2 + 5x + 4

Step 5: Verify the Standard Form

Verify that the quadratic equation is in standard form by checking the order of the terms and the coefficients.

Example:

x^2 + 5x + 4 → ax^2 + bx + c ( Correct!)

Examples and Practice

Let's practice writing quadratic equations in standard form with some examples:

• Example 1: Write the quadratic equation x^2 - 2x - 3 in standard form. Answer: x^2 - 2x - 3 → ax^2 + bx + c = x^2 - 2x - 3
• Example 2: Write the quadratic equation 2x^2 + 5x - 1 in standard form. Answer: 2x^2 + 5x - 1 → ax^2 + bx + c = 2x^2 + 5x - 1

Common Mistakes and Tips

When writing quadratic equations in standard form, be mindful of the following common mistakes and tips:

• Incorrect order: Make sure the terms are in the correct order: squared, linear, and constant.
• Missing or extra terms: Ensure all necessary terms are included, and no extra terms are added.
• Incorrect coefficients: Double-check the coefficients of each term to avoid errors.

By following these steps and tips, you'll become proficient in writing quadratic equations in standard form.

Conclusion and Next Steps

Writing quadratic equations in standard form is a fundamental skill in algebra, and with practice, you'll become more comfortable and confident. Remember to identify the quadratic equation, rearrange the terms, combine like terms, write in standard form, and verify the result.

To further improve your skills, try the following:

• Practice writing quadratic equations in standard form with different coefficients and terms.
• Solve quadratic equations using various methods, such as factoring, quadratic formula, or graphing.
• Apply quadratic equations to real-world problems and scenarios.

We hope this article has helped you understand the importance of standard form and provided a clear guide on how to write a quadratic in standard form. If you have any questions or need further clarification, please don't hesitate to ask.