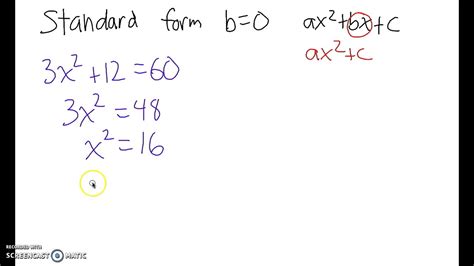Solving Standard Form Quadratic Equations Made Easy

Quick Links :

Understanding the Importance of Quadratic Equations

Quadratic equations are a fundamental concept in mathematics and are widely used in various fields such as physics, engineering, and computer science. These equations have the form of ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. Solving quadratic equations is a crucial skill for anyone who wants to excel in mathematics and related fields. In this article, we will focus on solving standard form quadratic equations, which are equations in the form of ax^2 + bx + c = 0.

The importance of solving quadratic equations cannot be overstated. These equations are used to model real-world problems, such as the trajectory of a projectile, the shape of a satellite dish, and the growth of a population. By solving quadratic equations, we can gain insights into the behavior of these systems and make informed decisions. Moreover, quadratic equations are a building block for more advanced mathematical concepts, such as calculus and linear algebra.

What are Standard Form Quadratic Equations?

Standard form quadratic equations are equations in the form of ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. In this form, a cannot be zero, and the equation is written in a specific order, with the x^2 term first, followed by the x term, and finally the constant term. For example, the equation 2x^2 + 5x - 3 = 0 is in standard form.

Standard form quadratic equations can be solved using various methods, including factoring, the quadratic formula, and graphing. In this article, we will focus on the quadratic formula, which is a powerful tool for solving quadratic equations.

The Quadratic Formula

The quadratic formula is a mathematical formula that provides the solutions to a quadratic equation in the form of ax^2 + bx + c = 0. The formula is:

x = (-b ± √(b^2 - 4ac)) / 2a

This formula can be used to solve any quadratic equation, regardless of the values of a, b, and c.

How to Solve Standard Form Quadratic Equations Using the Quadratic Formula

To solve a standard form quadratic equation using the quadratic formula, follow these steps:

1. Write the equation in standard form, ax^2 + bx + c = 0.
2. Identify the values of a, b, and c.
3. Plug these values into the quadratic formula: x = (-b ± √(b^2 - 4ac)) / 2a.
4. Simplify the expression by evaluating the square root and combining like terms.
5. Write the final solutions in the form x =...

For example, let's solve the equation 2x^2 + 5x - 3 = 0 using the quadratic formula.

1. Write the equation in standard form: 2x^2 + 5x - 3 = 0.
2. Identify the values of a, b, and c: a = 2, b = 5, and c = -3.
3. Plug these values into the quadratic formula: x = (-(5) ± √((5)^2 - 4(2)(-3))) / 2(2).
4. Simplify the expression: x = (-5 ± √(25 + 24)) / 4.
5. Write the final solutions: x = (-5 ± √49) / 4, which simplifies to x = (-5 ± 7) / 4.

Therefore, the solutions to the equation 2x^2 + 5x - 3 = 0 are x = (-5 + 7) / 4 = 1/2 and x = (-5 - 7) / 4 = -3.

Practical Applications of Solving Quadratic Equations

Solving quadratic equations has numerous practical applications in various fields. Here are a few examples:

1. Projectile Motion: Quadratic equations are used to model the trajectory of a projectile under the influence of gravity. By solving these equations, we can determine the maximum height, range, and time of flight of the projectile.
2. Electrical Engineering: Quadratic equations are used to analyze and design electrical circuits. By solving these equations, we can determine the current, voltage, and impedance of the circuit.
3. Computer Science: Quadratic equations are used in computer graphics to create smooth curves and surfaces. By solving these equations, we can create realistic models of objects and environments.
4. Physics: Quadratic equations are used to model the motion of objects under the influence of friction, gravity, and other forces. By solving these equations, we can determine the position, velocity, and acceleration of the object.

Conclusion: Mastering the Art of Solving Quadratic Equations

Solving standard form quadratic equations is a fundamental skill that requires practice and patience. By mastering the quadratic formula and understanding the practical applications of solving quadratic equations, you can become proficient in solving these equations and unlock a world of mathematical possibilities.

We encourage you to practice solving quadratic equations using the quadratic formula and explore the various practical applications of these equations. Share your experiences, ask questions, and engage with others who are passionate about mathematics.

FAQ Section: