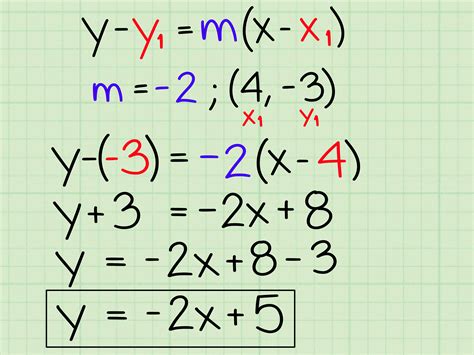5 Easy Ways To Rewrite In Slope Intercept Form

Quick Links :

When it comes to working with linear equations, being able to rewrite them in slope-intercept form is an essential skill. Slope-intercept form, which is expressed as y = mx + b, is a way of writing linear equations that clearly shows the slope (m) and the y-intercept (b) of the line. Mastering this skill can make solving and graphing linear equations much easier.

One of the main reasons slope-intercept form is so useful is that it allows you to easily identify the slope and y-intercept of a line, which can be used to graph the line and solve problems involving linear equations. Additionally, being able to rewrite linear equations in slope-intercept form can help you to identify the relationships between different variables and make it easier to solve systems of linear equations.

However, rewriting linear equations in slope-intercept form can sometimes be tricky. In this article, we will explore five easy ways to rewrite linear equations in slope-intercept form.

Method 1: Using the Slope Formula

One way to rewrite a linear equation in slope-intercept form is to use the slope formula. The slope formula is given by:

m = (y2 - y1) / (x2 - x1)

Where (x1, y1) and (x2, y2) are two points on the line.

Once you have found the slope, you can use it to rewrite the equation in slope-intercept form. For example, let's say we have the equation:

2x + 3y = 7

We can use the slope formula to find the slope of the line by choosing two points on the line, such as (0, 7/3) and (1, 2). Plugging these points into the slope formula, we get:

m = (2 - 7/3) / (1 - 0) = 1/3

Now that we have the slope, we can rewrite the equation in slope-intercept form as:

y = (1/3)x + 7/3

Method 2: Using the Point-Slope Form

Another way to rewrite a linear equation in slope-intercept form is to use the point-slope form. The point-slope form is given by:

y - y1 = m(x - x1)

Where (x1, y1) is a point on the line and m is the slope.

Once you have found the slope and a point on the line, you can use the point-slope form to rewrite the equation in slope-intercept form. For example, let's say we have the equation:

x - 2y = 3

We can rewrite this equation in point-slope form by choosing a point on the line, such as (3, 0). Plugging this point into the point-slope form, we get:

y - 0 = (1/2)(x - 3)

Simplifying this equation, we get:

y = (1/2)x - 3/2

Method 3: Using the Standard Form

The standard form of a linear equation is given by:

Ax + By = C

Where A, B, and C are constants.

To rewrite a linear equation in slope-intercept form from standard form, we need to solve the equation for y. For example, let's say we have the equation:

2x + 3y = 7

We can solve this equation for y by subtracting 2x from both sides and then dividing both sides by 3:

3y = -2x + 7

y = (-2/3)x + 7/3

Method 4: Using the Intercept Form

The intercept form of a linear equation is given by:

x/a + y/b = 1

Where a and b are the x-intercept and y-intercept of the line, respectively.

To rewrite a linear equation in slope-intercept form from intercept form, we need to solve the equation for y. For example, let's say we have the equation:

x/2 + y/3 = 1

We can solve this equation for y by multiplying both sides by 3 and then subtracting x from both sides:

y = -3x/2 + 3

Method 5: Using a Graph

Finally, we can also rewrite a linear equation in slope-intercept form by graphing the equation and identifying the slope and y-intercept. For example, let's say we have the equation:

x - 2y = 3

We can graph this equation by plotting two points on the line and drawing a line through them. Once we have graphed the equation, we can identify the slope and y-intercept by looking at the graph.

For example, let's say we graph the equation and find that the slope is 1/2 and the y-intercept is -3/2. We can then use this information to rewrite the equation in slope-intercept form as:

y = (1/2)x - 3/2

As you can see, there are several ways to rewrite linear equations in slope-intercept form. Whether you use the slope formula, point-slope form, standard form, intercept form, or a graph, the key is to identify the slope and y-intercept of the line and use this information to rewrite the equation in slope-intercept form.

By mastering these five methods, you'll be able to rewrite linear equations in slope-intercept form with ease, making it easier to solve and graph linear equations.

We hope this article has been helpful in explaining the different methods for rewriting linear equations in slope-intercept form. If you have any questions or need further clarification, please don't hesitate to ask.