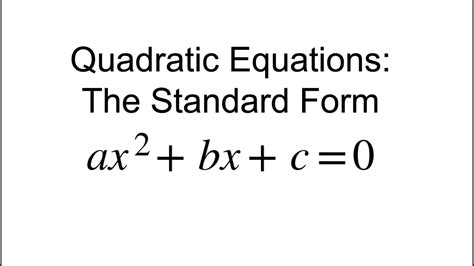Quadratic functions are a fundamental concept in algebra, and understanding them is crucial for solving problems in mathematics, physics, engineering, and other fields. One of the most common forms of quadratic functions is the standard form, which is essential for graphing and analyzing these functions. In this article, we will explore the world of quadratic functions in standard form, and provide you with a comprehensive guide on how to work with them easily.

What is a Quadratic Function in Standard Form?
A quadratic function in standard form is written in the following format:
ax^2 + bx + c = 0
where a, b, and c are constants, and x is the variable. The standard form is also known as the general form or the ax^2 + bx + c form. In this form, a cannot be zero, and the equation represents a parabola when graphed.
Why is the Standard Form Important?
The standard form is essential for several reasons:
- It allows us to easily identify the vertex, axis of symmetry, and x-intercepts of the parabola.
- It enables us to graph the parabola using simple transformations.
- It provides a way to solve quadratic equations using factoring, the quadratic formula, or other methods.
How to Write Quadratic Functions in Standard Form
There are several ways to write quadratic functions in standard form, depending on the given information. Here are a few examples:
Example 1: Writing a Quadratic Function from a Table of Values
Suppose we have a table of values that represents a quadratic function:
| x | y |
|---|---|
| -2 | 3 |
| -1 | 2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
We can write a quadratic function in standard form by finding the equation of the parabola that passes through these points. After analyzing the data, we find that the equation is:
x^2 + 2x + 1 = 0
Example 2: Writing a Quadratic Function from a Graph
Suppose we have a graph of a parabola that opens upward, with a vertex at (-2, 1). We can write a quadratic function in standard form by using the vertex form:
y = a(x - h)^2 + k
where (h, k) is the vertex. In this case, h = -2 and k = 1. Substituting these values, we get:
y = a(x + 2)^2 + 1
To find the value of a, we can use the fact that the parabola passes through the point (0, 3). Substituting x = 0 and y = 3, we get:
3 = a(0 + 2)^2 + 1 3 = 4a + 1 4a = 2 a = 1/2
Therefore, the equation of the parabola in standard form is:
y = (1/2)x^2 + 2x + 1

How to Graph Quadratic Functions in Standard Form
Graphing quadratic functions in standard form is relatively easy. Here are the steps:
- Identify the vertex, axis of symmetry, and x-intercepts from the equation.
- Plot the vertex and x-intercepts on the graph.
- Use the axis of symmetry to reflect the points across the axis.
- Connect the points to form a smooth curve.
Example: Graphing a Quadratic Function
Suppose we want to graph the quadratic function:
x^2 + 4x + 4 = 0
We can identify the vertex, axis of symmetry, and x-intercepts as follows:
- Vertex: (-2, 0)
- Axis of symmetry: x = -2
- X-intercepts: (-2, 0) and (0, 4)
Plotting these points and reflecting them across the axis of symmetry, we get the graph:

Conclusion
In this article, we have explored the world of quadratic functions in standard form. We have seen how to write these functions, graph them, and analyze their properties. By mastering the standard form, you can solve a wide range of problems in mathematics, physics, and engineering. We hope this article has been informative and helpful. If you have any questions or comments, please feel free to share them below.
What is the standard form of a quadratic function?
+The standard form of a quadratic function is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable.
Why is the standard form important?
+The standard form is essential for identifying the vertex, axis of symmetry, and x-intercepts of a parabola, as well as for graphing and analyzing the function.
How do I graph a quadratic function in standard form?
+To graph a quadratic function in standard form, identify the vertex, axis of symmetry, and x-intercepts, plot these points, and reflect them across the axis of symmetry to form a smooth curve.