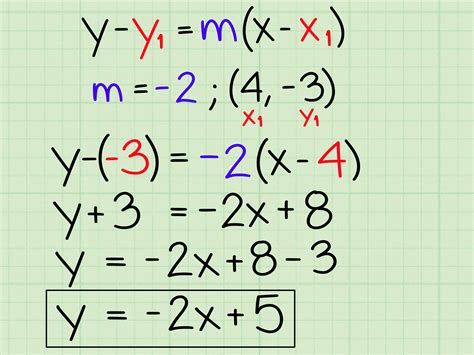Convert To Slope Intercept Form Made Easy

Quick Links :

The slope-intercept form of a linear equation is one of the most common and versatile ways to express a line in mathematics. It's widely used in various fields, including physics, engineering, and economics, to model real-world phenomena. In this article, we'll explore the concept of converting to slope-intercept form, its importance, and provide a step-by-step guide on how to do it easily.

What is Slope-Intercept Form?

The slope-intercept form of a linear equation is given by the equation y = mx + b, where:

• m is the slope of the line, which represents the rate of change of the dependent variable (y) with respect to the independent variable (x).
• b is the y-intercept, which is the point where the line intersects the y-axis.

This form is useful because it allows us to easily identify the slope and y-intercept of a line, which are essential in understanding the behavior of the line.

Why is Converting to Slope-Intercept Form Important?

Converting to slope-intercept form is important because it provides a clear and concise way to express a linear equation. This form is useful in various applications, such as:

• Graphing lines: By converting to slope-intercept form, we can easily graph a line by plotting the y-intercept and using the slope to determine the direction of the line.
• Solving systems of equations: The slope-intercept form is useful in solving systems of linear equations, as it allows us to easily identify the point of intersection between two lines.
• Analyzing functions: The slope-intercept form is useful in analyzing functions, as it allows us to easily identify the rate of change of a function and its y-intercept.

How to Convert to Slope-Intercept Form

Converting to slope-intercept form is a straightforward process that involves a few simple steps. Here's a step-by-step guide:

1. Start with the standard form: Begin with the standard form of a linear equation, which is Ax + By = C, where A, B, and C are constants.
2. Subtract By from both sides: Subtract By from both sides of the equation to isolate y. This will give you Ax = -By + C.
3. Divide both sides by A: Divide both sides of the equation by A to solve for y. This will give you y = (-B/A)x + C/A.
4. Simplify the equation: Simplify the equation by combining like terms and rewriting it in the slope-intercept form, which is y = mx + b.

Example 1: Converting to Slope-Intercept Form

Suppose we have the equation 2x + 3y = 5, and we want to convert it to slope-intercept form. Here's how we can do it:

1. Subtract 2x from both sides: 3y = -2x + 5
2. Divide both sides by 3: y = (-2/3)x + 5/3
3. Simplify the equation: y = (-2/3)x + 5/3

Tips and Tricks for Converting to Slope-Intercept Form

Here are some tips and tricks for converting to slope-intercept form:

• Check your work: Always check your work by plugging your solution back into the original equation to ensure that it's true.
• Simplify your equation: Simplify your equation by combining like terms and rewriting it in the slope-intercept form.
• Use online tools: Use online tools, such as graphing calculators or equation solvers, to check your work and visualize the graph of the line.

Common Mistakes to Avoid When Converting to Slope-Intercept Form

Here are some common mistakes to avoid when converting to slope-intercept form:

• Forgetting to simplify the equation: Forgetting to simplify the equation can lead to errors and make it difficult to graph the line.
• Incorrectly dividing or subtracting: Incorrectly dividing or subtracting can lead to errors and make it difficult to graph the line.
• Not checking your work: Not checking your work can lead to errors and make it difficult to graph the line.

Real-World Applications of Converting to Slope-Intercept Form

Converting to slope-intercept form has numerous real-world applications, including:

• Physics and engineering: Converting to slope-intercept form is useful in physics and engineering, where it's used to model the motion of objects and the behavior of systems.
• Economics: Converting to slope-intercept form is useful in economics, where it's used to model the behavior of markets and the impact of policy changes.
• Computer science: Converting to slope-intercept form is useful in computer science, where it's used to model the behavior of algorithms and the performance of systems.

Conclusion

Converting to slope-intercept form is a fundamental skill in mathematics that has numerous real-world applications. By following the steps outlined in this article, you can easily convert to slope-intercept form and gain a deeper understanding of linear equations. Remember to always check your work and simplify your equation to ensure that you get the correct solution.