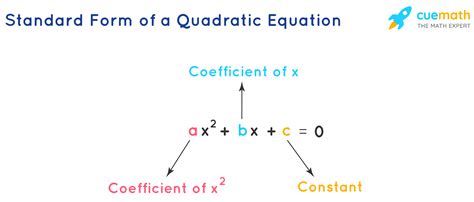
Quadratic Equations: Standard Form Made Easy

Quick Links :

Hide

Quadratic equations are a fundamental concept in algebra, and their standard form is a crucial aspect of solving them. However, many students find it challenging to grasp the concept of standard form, leading to difficulties in solving quadratic equations. In this article, we will break down the concept of standard form, its importance, and provide practical examples to make it easy to understand.

What is Standard Form?

A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. The standard form is essential because it allows us to identify the coefficients a, b, and c, which are crucial in solving the equation.

Why is Standard Form Important?

The standard form is vital in solving quadratic equations because it enables us to use various methods, such as factoring, the quadratic formula, and graphing. By identifying the coefficients a, b, and c, we can determine the nature of the solutions, the vertex of the parabola, and the axis of symmetry.

How to Write a Quadratic Equation in Standard Form

To write a quadratic equation in standard form, follow these steps:

1. Identify the variable (usually x) and the constants a, b, and c.
2. Rearrange the equation to have the variable squared (x^2) as the first term.
3. Combine like terms and simplify the equation.
4. Write the equation in the form ax^2 + bx + c = 0.

Example: Write the equation x^2 + 5x + 3 = 2x^2 - 4x - 1 in standard form.

Solution: Combine like terms and simplify the equation to get 3x^2 - 9x - 4 = 0.

Types of Quadratic Equations

There are several types of quadratic equations, including:

• Linear Quadratic Equations: These equations have a linear term (bx) and a constant term (c).
• Quadratic Equations with No Linear Term: These equations have only a squared term (ax^2) and a constant term (c).
• Quadratic Equations with No Constant Term: These equations have only a squared term (ax^2) and a linear term (bx).

Solving Quadratic Equations

There are several methods to solve quadratic equations, including:

• Factoring: This method involves factoring the quadratic expression into two binomials.
• Quadratic Formula: This method involves using the quadratic formula x = (-b ± √(b^2 - 4ac)) / 2a to find the solutions.
• Graphing: This method involves graphing the quadratic function and finding the x-intercepts.

Real-World Applications of Quadratic Equations

Quadratic equations have numerous real-world applications, including:

• Physics: Quadratic equations are used to describe the motion of objects under the influence of gravity.
• Engineering: Quadratic equations are used to design and optimize systems, such as bridges and electronic circuits.
• Economics: Quadratic equations are used to model economic systems and make predictions about economic behavior.

Conclusion

In conclusion, standard form is a crucial aspect of quadratic equations, and understanding it is essential for solving these equations. By following the steps outlined in this article, you can write quadratic equations in standard form and use various methods to solve them. Remember, practice makes perfect, so be sure to practice solving quadratic equations to become proficient.

We hope this article has helped you understand quadratic equations in standard form. Share your thoughts and questions in the comments section below.