Finding X-Intercept From Vertex Form Made Easy

Quick Links :

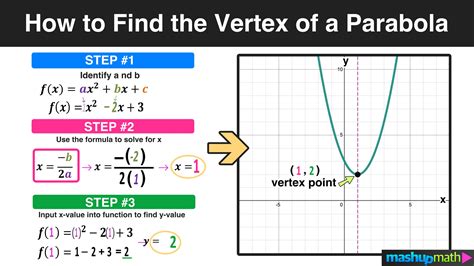
Finding the x-intercept of a quadratic function can be a daunting task, especially when the equation is given in vertex form. However, with a few simple steps, you can easily find the x-intercept of a quadratic function, even when it's in vertex form. In this article, we'll explore the concept of vertex form, how to find the x-intercept, and provide some practical examples to help you understand the process.

Understanding Vertex Form

Vertex form is a way of expressing a quadratic function in the form f(x) = a(x-h)^2 + k, where (h, k) is the vertex of the parabola. This form is particularly useful when you need to find the vertex of a quadratic function, but it can be challenging to find the x-intercept.

What is the X-Intercept?

The x-intercept is the point where the graph of a function crosses the x-axis. It's an essential concept in algebra and is used to solve equations and graph functions. In the context of quadratic functions, the x-intercept is the point where the parabola intersects the x-axis.

How to Find the X-Intercept From Vertex Form

To find the x-intercept of a quadratic function in vertex form, you need to follow these steps:

1. Identify the vertex (h, k) of the parabola.
2. Set f(x) equal to 0 and solve for x.
3. Simplify the equation and find the value of x.

Here's an example to illustrate this process:

Suppose we have a quadratic function in vertex form: f(x) = 2(x-3)^2 + 1.

To find the x-intercept, we set f(x) equal to 0:

2(x-3)^2 + 1 = 0

Next, we simplify the equation:

2(x-3)^2 = -1

Now, we solve for x:

(x-3)^2 = -1/2

x-3 = ±√(-1/2)

x = 3 ± √(-1/2)

Since we can't take the square root of a negative number, this equation has no real solutions. Therefore, the x-intercept does not exist for this quadratic function.

Practical Examples

Let's consider a few more examples to illustrate the process of finding the x-intercept from vertex form:

Example 1:

f(x) = (x+2)^2 - 4

To find the x-intercept, we set f(x) equal to 0:

(x+2)^2 - 4 = 0

Next, we simplify the equation:

(x+2)^2 = 4

Now, we solve for x:

x+2 = ±√4

x = -2 ± 2

Therefore, the x-intercepts are x = -4 and x = 0.

Example 2:

f(x) = -3(x-1)^2 + 2

To find the x-intercept, we set f(x) equal to 0:

-3(x-1)^2 + 2 = 0

Next, we simplify the equation:

-3(x-1)^2 = -2

Now, we solve for x:

(x-1)^2 = 2/3

x-1 = ±√(2/3)

x = 1 ± √(2/3)

Therefore, the x-intercepts are x = 1 + √(2/3) and x = 1 - √(2/3).

Benefits of Finding the X-Intercept

Finding the x-intercept of a quadratic function has several benefits, including:

• Solving equations: The x-intercept can be used to solve equations by setting the function equal to 0 and solving for x.
• Graphing functions: The x-intercept can be used to graph functions by plotting the points where the function intersects the x-axis.
• Analyzing functions: The x-intercept can be used to analyze functions by identifying the points where the function changes direction.

Common Mistakes to Avoid

When finding the x-intercept from vertex form, there are several common mistakes to avoid:

• Forgetting to set f(x) equal to 0
• Simplifying the equation incorrectly
• Solving for x incorrectly

By avoiding these mistakes and following the steps outlined above, you can easily find the x-intercept of a quadratic function in vertex form.

Conclusion and Final Thoughts

In conclusion, finding the x-intercept of a quadratic function in vertex form is a straightforward process that requires setting f(x) equal to 0, simplifying the equation, and solving for x. By following these steps and avoiding common mistakes, you can easily find the x-intercept of a quadratic function. Remember to always check your work and use practical examples to illustrate the process.

We hope this article has been helpful in explaining the concept of finding the x-intercept from vertex form. If you have any questions or comments, please feel free to share them below.