3 Easy Ways To Find Vertex In Intercept Form

Quick Links :

When it comes to graphing and analyzing functions, understanding the different forms of a quadratic equation is crucial. One of these forms is the intercept form, which provides valuable insights into the graph's x-intercepts. However, finding the vertex of a quadratic function in intercept form can be a bit more challenging. In this article, we will explore three easy ways to find the vertex in intercept form, making it simpler for you to work with quadratic functions.

Why is finding the vertex important?

The vertex of a quadratic function is the lowest or highest point on its graph, depending on the direction of the parabola. It is essential to find the vertex because it helps you understand the function's behavior, identify its maximum or minimum value, and make predictions about the graph's shape. In real-world applications, the vertex can represent the maximum or minimum value of a quantity, such as the maximum height of a projectile or the minimum cost of a production process.

Method 1: Completing the Square

The first method to find the vertex in intercept form is by completing the square. This method involves rewriting the quadratic function in vertex form by manipulating the equation.

To complete the square, follow these steps:

1. Start with the intercept form of the quadratic function: y = a(x - p)(x - q)
2. Expand the equation: y = a(x^2 - px - qx + pq)
3. Rearrange the terms: y = a(x^2 - (p + q)x + pq)
4. Complete the square by adding and subtracting (p + q)^2/4 inside the parentheses: y = a(x^2 - (p + q)x + (p + q)^2/4 - (p + q)^2/4 + pq)
5. Simplify the equation: y = a(x - (p + q)/2)^2 - a(p + q)^2/4 + apq

The vertex form of a quadratic function is y = a(x - h)^2 + k, where (h, k) is the vertex. By comparing this form with the completed square equation, we can identify the vertex:

h = (p + q)/2 and k = -a(p + q)^2/4 + apq

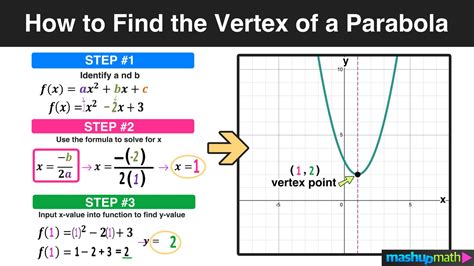
Method 2: Using the Formula

The second method to find the vertex in intercept form is by using a formula. This formula is derived from the fact that the x-coordinate of the vertex is the average of the x-intercepts.

The formula for the x-coordinate of the vertex is:

h = (p + q)/2

To find the y-coordinate of the vertex, substitute h into the original equation:

k = a(h - p)(h - q)

Simplify the equation to find the value of k.

Method 3: Graphical Method

The third method to find the vertex in intercept form is by using a graphical approach. This method involves graphing the quadratic function and identifying the vertex from the graph.

To use the graphical method, follow these steps:

1. Graph the quadratic function using its x-intercepts and the fact that it is a parabola.
2. Identify the vertex from the graph by finding the lowest or highest point.
3. Record the coordinates of the vertex.

Conclusion

Finding the vertex of a quadratic function in intercept form can be a bit challenging, but using one of the three methods outlined above can make it easier. Whether you prefer completing the square, using a formula, or graphing the function, each method provides a unique approach to finding the vertex. By mastering these methods, you will become more proficient in working with quadratic functions and be able to analyze and graph them with confidence.

Now that you have learned these three easy ways to find the vertex in intercept form, try practicing with some examples to reinforce your understanding. If you have any questions or need further clarification, feel free to ask in the comments below. Share this article with your friends and classmates who may also find it helpful.