Find Focus And Directrix From Vertex Form Easily

Quick Links :

Finding the focus and directrix of a parabola in vertex form is a fundamental concept in algebra and geometry. The vertex form of a parabola is given by the equation y = a(x - h)^2 + k, where (h, k) represents the coordinates of the vertex. In this article, we will explore the steps to find the focus and directrix from the vertex form of a parabola, and provide examples to illustrate the process.

Understanding the Vertex Form

The vertex form of a parabola provides valuable information about the parabola's shape and position. The vertex (h, k) represents the turning point of the parabola, and the value of 'a' determines the parabola's direction and width.

Recall the Formula for Focus and Directrix

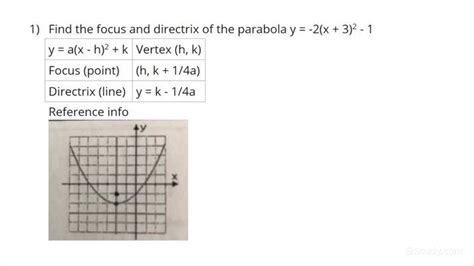
To find the focus and directrix of a parabola in vertex form, we need to recall the following formulas:

• Focus: (h, k + 1/(4a))
• Directrix: y = k - 1/(4a)

These formulas are derived from the definition of a parabola as the set of points equidistant from the focus and directrix.

Step-by-Step Process to Find Focus and Directrix

To find the focus and directrix of a parabola in vertex form, follow these steps:

1. Identify the values of 'a', 'h', and 'k' from the given equation in vertex form.
2. Use the formula for the focus: (h, k + 1/(4a)). Plug in the values of 'h', 'k', and 'a' to find the coordinates of the focus.
3. Use the formula for the directrix: y = k - 1/(4a). Plug in the values of 'k' and 'a' to find the equation of the directrix.

Example 1: Finding Focus and Directrix

Consider the parabola given by the equation y = 2(x - 3)^2 + 1.

• Identify the values: a = 2, h = 3, and k = 1.
• Find the focus: (h, k + 1/(4a)) = (3, 1 + 1/(4*2)) = (3, 1 + 1/8) = (3, 1.125)
• Find the directrix: y = k - 1/(4a) = 1 - 1/(4*2) = 1 - 1/8 = 0.875

Special Cases and Considerations

When working with parabolas in vertex form, there are some special cases and considerations to keep in mind:

• If 'a' is positive, the parabola opens upward, and the focus lies above the vertex.
• If 'a' is negative, the parabola opens downward, and the focus lies below the vertex.
• If 'a' is zero, the parabola is a horizontal line, and there is no focus or directrix.

Example 2: Finding Focus and Directrix with a Negative 'a'

Consider the parabola given by the equation y = -3(x + 2)^2 - 4.

• Identify the values: a = -3, h = -2, and k = -4.
• Find the focus: (h, k + 1/(4a)) = (-2, -4 + 1/(4*(-3))) = (-2, -4 + (-1/12)) = (-2, -4.083)
• Find the directrix: y = k - 1/(4a) = -4 - 1/(4*(-3)) = -4 - (-1/12) = -3.917

Practical Applications and Real-World Examples

Parabolas and their focus and directrix have numerous practical applications in various fields, including:

• Architecture: Parabolas are used in the design of arches, bridges, and other structures.
• Engineering: Parabolas are used in the design of satellite dishes, mirrors, and other optical instruments.
• Physics: Parabolas are used to model the trajectory of projectiles and the path of light rays.

Conclusion

Finding the focus and directrix of a parabola in vertex form is a fundamental concept in algebra and geometry. By following the step-by-step process outlined in this article, you can easily find the focus and directrix of a parabola in vertex form. Remember to consider special cases and real-world applications, and practice with examples to reinforce your understanding.

We hope this article has been informative and helpful. If you have any questions or comments, please feel free to share them below.