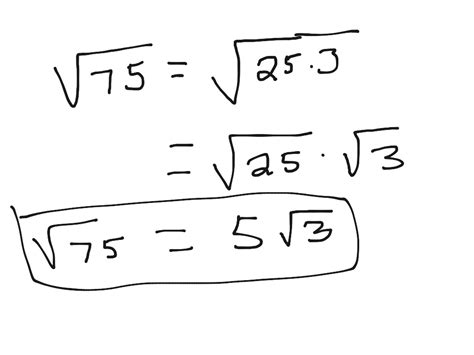Simplify The Square Root Of 75 In Radical Form

Quick Links :

The concept of simplifying square roots in radical form is a fundamental idea in algebra. To simplify the square root of 75, we'll break it down into a product of prime factors and then identify perfect squares that can be extracted from the radical.

First, let's express 75 as a product of prime factors:

75 = 3 × 5 × 5

Now, we can rewrite the square root of 75 using these prime factors:

√75 = √(3 × 5 × 5)

Since we have a pair of 5s, which is a perfect square, we can extract one of the 5s from the radical:

√75 = √(3 × 5²)

Using the property of square roots that allows us to split a product into separate square roots, we get:

√75 = √3 × √5²

Since the square root of 5² is simply 5, we can simplify further:

√75 = √3 × 5

Combining the square root of 3 with the factor of 5, we get:

√75 = 5√3

So, the simplified square root of 75 in radical form is 5√3.

What are Square Roots?

A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 × 4 = 16. Square roots can be expressed in radical form, which involves the √ symbol, or in decimal form, which is a numerical value.

Types of Square Roots

There are two types of square roots: perfect squares and imperfect squares. Perfect squares are numbers that have an integer square root, such as 16, 25, and 36. Imperfect squares, on the other hand, are numbers that do not have an integer square root, such as 75, 90, and 120.

Simplifying Square Roots

Simplifying square roots involves breaking down a number into its prime factors and then identifying perfect squares that can be extracted from the radical. This process can be applied to both perfect and imperfect squares.

For example, the square root of 100 can be simplified as follows:

√100 = √(10 × 10)

= √10²

= 10

In this case, we were able to simplify the square root of 100 to 10, because 10 is a perfect square.

Why Simplify Square Roots?

Simplifying square roots is important in mathematics and science, as it allows us to express numbers in a more compact and readable form. Simplified square roots can also be used to solve equations and inequalities, and to graph functions.

Radical Form vs. Decimal Form

Square roots can be expressed in either radical form or decimal form. Radical form involves the √ symbol, while decimal form is a numerical value.

For example, the square root of 2 can be expressed in radical form as √2, or in decimal form as 1.41.

Advantages of Radical Form

Radical form has several advantages over decimal form:

• It provides an exact representation of the square root, without rounding errors.
• It can be used to simplify complex expressions and equations.
• It is often more compact and readable than decimal form.

Disadvantages of Radical Form

However, radical form also has some disadvantages:

• It can be more difficult to understand and work with, especially for large numbers.
• It may not provide a clear indication of the size or magnitude of the number.
• It can be less familiar to non-mathematicians, who may be more accustomed to decimal form.

Conclusion

In conclusion, simplifying square roots in radical form is an important concept in mathematics and science. By breaking down a number into its prime factors and extracting perfect squares, we can simplify complex expressions and equations. Radical form has several advantages over decimal form, including exact representation, compactness, and readability. However, it also has some disadvantages, such as difficulty of understanding and familiarity. By understanding the concepts and techniques of simplifying square roots, we can improve our mathematical skills and problem-solving abilities.