2 Easy Steps To Write 47 In Expanded Form

Quick Links :

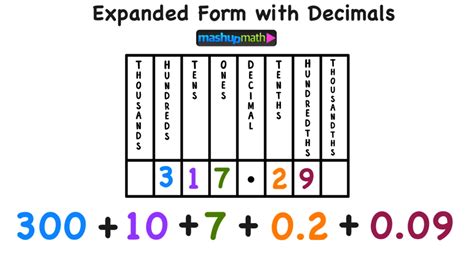
The concept of expanded form in mathematics refers to the process of expressing a number in a way that shows the value of each digit. This can be a useful tool for students and mathematicians alike, as it allows for a deeper understanding of the structure of numbers and can help to simplify complex calculations.

The number 47 is a relatively small number, and expressing it in expanded form is a straightforward process that can be completed in just two easy steps.

Understanding the Basics of Expanded Form

Before we dive into the specifics of expressing 47 in expanded form, let's take a moment to review the basics of this concept. Expanded form is a way of expressing a number that shows the value of each digit. This is done by multiplying each digit by its corresponding place value (ones, tens, hundreds, etc.) and then adding up the results.

For example, the number 456 can be expressed in expanded form as:

4 x 100 = 400 5 x 10 = 50 6 x 1 = 6

Adding up these values gives us the original number:

400 + 50 + 6 = 456

This is a basic example, but it illustrates the concept of expanded form nicely.

Step 1: Break Down the Number into Its Component Parts

To express 47 in expanded form, we need to break down the number into its component parts. This means identifying the value of each digit and its corresponding place value.

In this case, we have:

4 (tens place) 7 (ones place)

We can then multiply each digit by its corresponding place value:

4 x 10 = 40 7 x 1 = 7

Step 2: Combine the Values to Get the Final Answer

Now that we have the values of each digit, we can combine them to get the final answer.

40 + 7 = 47

And that's it! We have successfully expressed 47 in expanded form.

The Benefits of Expanded Form

Expressing numbers in expanded form can be a useful tool for a variety of mathematical applications. Here are just a few examples:

• Improved understanding of place value: Expanded form helps to illustrate the concept of place value, which is a fundamental building block of mathematics.
• Simplified calculations: By breaking down numbers into their component parts, expanded form can make complex calculations easier to manage.
• Enhanced problem-solving skills: Expanded form can help students develop their problem-solving skills by providing a framework for breaking down complex problems into manageable parts.

Common Applications of Expanded Form

Expanded form has a wide range of applications in mathematics and beyond. Here are just a few examples:

• Basic arithmetic: Expanded form is used extensively in basic arithmetic operations such as addition, subtraction, multiplication, and division.
• Algebra: Expanded form is used to simplify algebraic expressions and equations.
• Real-world applications: Expanded form is used in a variety of real-world applications, such as finance, science, and engineering.

Conclusion and Call to Action

Expressing 47 in expanded form is a simple process that can be completed in just two easy steps. By breaking down the number into its component parts and combining the values, we can gain a deeper understanding of the structure of numbers and improve our mathematical skills.

We hope this article has been informative and helpful. If you have any questions or comments, please don't hesitate to reach out. We'd love to hear from you!