Mastering Quadratics: 7 Essential Graphing Tips

Quick Links :

Understanding quadratics is a fundamental aspect of algebra and mathematics as a whole. Quadratic equations, which are polynomial equations of degree two, are used to model a wide range of phenomena in physics, engineering, economics, and other fields. Graphing quadratics, in particular, is an essential skill for visualizing and analyzing these phenomena. However, many students struggle with graphing quadratics due to a lack of understanding of the underlying concepts or poor technique.

In this article, we will explore seven essential graphing tips to help you master quadratics. Whether you are a student looking to improve your grades or a professional seeking to refresh your knowledge, these tips will provide you with the skills and confidence you need to tackle even the most complex quadratic equations.

Tip 1: Understand the General Form of a Quadratic Equation

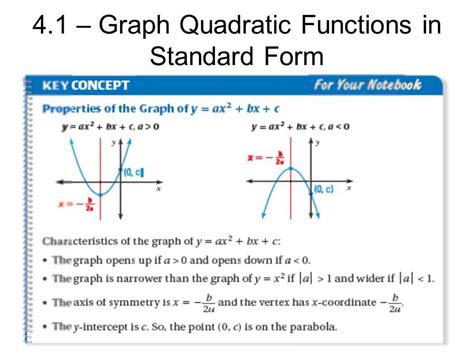
The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants. Understanding the role of each coefficient is crucial for graphing quadratics. The coefficient "a" determines the direction and width of the parabola, while "b" affects the position of the vertex. The constant term "c" shifts the parabola up or down.

Key Takeaway

• The value of "a" determines the direction of the parabola (opens upward if a > 0, downward if a < 0).
• The value of "b" affects the position of the vertex (shifts the parabola left or right).
• The value of "c" shifts the parabola up or down.

Tip 2: Identify the Vertex of the Parabola

The vertex of a parabola is the lowest or highest point on the graph. Identifying the vertex is essential for graphing quadratics, as it provides a reference point for sketching the rest of the parabola. The vertex can be found using the formula x = -b / 2a.

Key Takeaway

• The vertex of a parabola is the lowest or highest point on the graph.
• The vertex can be found using the formula x = -b / 2a.

Tip 3: Determine the Axis of Symmetry

The axis of symmetry is an imaginary line that passes through the vertex of the parabola. It is essential for graphing quadratics, as it divides the parabola into two symmetrical halves. The axis of symmetry can be found using the formula x = -b / 2a.

Key Takeaway

• The axis of symmetry is an imaginary line that passes through the vertex of the parabola.
• The axis of symmetry can be found using the formula x = -b / 2a.

Tip 4: Use the x-Intercepts to Sketch the Parabola

The x-intercepts of a parabola are the points where the parabola crosses the x-axis. Using the x-intercepts to sketch the parabola can help you ensure that the graph is accurate and symmetrical.

Key Takeaway

• The x-intercepts of a parabola are the points where the parabola crosses the x-axis.
• Using the x-intercepts to sketch the parabola can help you ensure that the graph is accurate and symmetrical.

Tip 5: Analyze the Leading Coefficient

The leading coefficient is the coefficient of the x^2 term in a quadratic equation. Analyzing the leading coefficient can help you determine the direction and width of the parabola.

Key Takeaway

• The leading coefficient determines the direction and width of the parabola.
• A positive leading coefficient indicates that the parabola opens upward.
• A negative leading coefficient indicates that the parabola opens downward.

Tip 6: Use Technology to Graph Quadratics

Graphing calculators and computer software can be used to graph quadratics quickly and accurately. Using technology can help you visualize the parabola and identify key features such as the vertex, axis of symmetry, and x-intercepts.

Key Takeaway

• Graphing calculators and computer software can be used to graph quadratics quickly and accurately.
• Using technology can help you visualize the parabola and identify key features.

Tip 7: Practice, Practice, Practice!

The key to mastering quadratics is practice. The more you practice graphing quadratics, the more comfortable you will become with the process. Start with simple equations and gradually work your way up to more complex ones.

Key Takeaway

• Practice is essential for mastering quadratics.
• Start with simple equations and gradually work your way up to more complex ones.

Now that you have read these seven essential graphing tips, it's time to put them into practice. Take a few minutes to practice graphing quadratics using the tips outlined above. With practice and patience, you will become proficient in graphing quadratics and be able to tackle even the most complex equations.

We hope this article has been informative and helpful. If you have any questions or need further clarification on any of the tips, please don't hesitate to ask. Share your thoughts and experiences in the comments section below.