5 Ways To Master Graphing Lines In Slope Intercept Form

Quick Links :

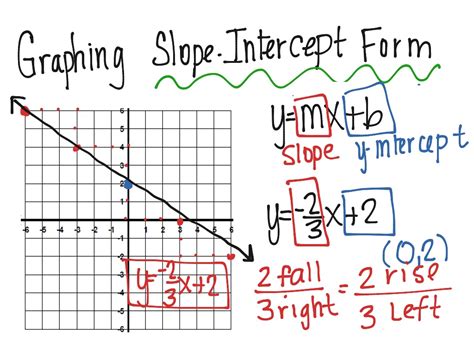
Graphing lines in slope-intercept form is a fundamental concept in algebra and mathematics. Mastering this skill can help you solve problems in various fields, including physics, engineering, and economics. Slope-intercept form is a way of writing linear equations in the form y = mx + b, where m is the slope and b is the y-intercept. In this article, we will explore five ways to master graphing lines in slope-intercept form.

Understanding Slope-Intercept Form

To start, it's essential to understand the components of slope-intercept form. The slope (m) represents the rate of change of the line, while the y-intercept (b) is the point where the line crosses the y-axis. When graphing lines in slope-intercept form, you need to identify these two values to plot the line accurately.

Why Slope-Intercept Form Matters

Slope-intercept form is a powerful tool for graphing lines because it provides a clear and concise way to represent linear relationships. By understanding the slope and y-intercept, you can:

• Identify the direction and steepness of the line
• Determine the point where the line crosses the y-axis
• Write the equation of the line in a compact and readable form

Method 1: Plotting Points Using Slope-Intercept Form

One way to master graphing lines in slope-intercept form is to plot points using the slope and y-intercept. To do this:

1. Identify the y-intercept (b) and plot the point (0, b) on the graph.
2. Use the slope (m) to determine the direction and steepness of the line.
3. Plot additional points by moving up or down from the y-intercept, using the slope to guide you.
4. Connect the points to form a line.

Example: Plotting a Line Using Slope-Intercept Form

Suppose we want to graph the line y = 2x + 3. To do this:

1. Plot the point (0, 3) on the graph, which represents the y-intercept.
2. Use the slope (m = 2) to determine the direction and steepness of the line.
3. Plot additional points by moving up from the y-intercept, using the slope to guide you. For example, the point (1, 5) would be plotted by moving up 2 units from the y-intercept.
4. Connect the points to form a line.

Method 2: Using the Slope Formula

Another way to master graphing lines in slope-intercept form is to use the slope formula. The slope formula is:

m = (y2 - y1) / (x2 - x1)

By using the slope formula, you can calculate the slope of the line and then use it to graph the line in slope-intercept form.

Example: Calculating Slope Using the Slope Formula

Suppose we want to calculate the slope of the line that passes through the points (2, 3) and (4, 5). To do this:

1. Plug the values into the slope formula: m = (5 - 3) / (4 - 2)
2. Simplify the equation: m = 2 / 2 = 1
3. Use the slope to graph the line in slope-intercept form.

Method 3: Graphing Lines Using a Table of Values

A third way to master graphing lines in slope-intercept form is to use a table of values. A table of values is a list of x-values and corresponding y-values that can be used to graph a line.

Example: Graphing a Line Using a Table of Values

Suppose we want to graph the line y = 2x + 1. To do this:

1. Create a table of values with x-values and corresponding y-values.
2. Plot the points on the graph using the table of values.
3. Connect the points to form a line.

Method 4: Using Graphing Calculators or Software

A fourth way to master graphing lines in slope-intercept form is to use graphing calculators or software. Graphing calculators and software can quickly and accurately graph lines in slope-intercept form.

Example: Graphing a Line Using a Graphing Calculator

Suppose we want to graph the line y = 3x - 2. To do this:

1. Enter the equation into the graphing calculator or software.
2. Adjust the window settings to view the entire graph.
3. Use the calculator or software to identify key features of the graph, such as the y-intercept and slope.

Method 5: Practicing with Real-World Applications

A final way to master graphing lines in slope-intercept form is to practice with real-world applications. Real-world applications can help you see the relevance and importance of graphing lines in slope-intercept form.

Example: Modeling a Real-World Situation with a Linear Equation

Suppose a company produces and sells a product, and the cost of producing the product is directly proportional to the number of units produced. To model this situation using a linear equation, you could use the slope-intercept form:

y = mx + b

where y is the cost, x is the number of units produced, m is the slope, and b is the y-intercept.

By mastering graphing lines in slope-intercept form, you can better understand and analyze real-world situations, making you a more effective problem solver.

We hope this article has provided you with a comprehensive guide to mastering graphing lines in slope-intercept form. Remember to practice regularly and apply your knowledge to real-world situations to become proficient in graphing lines. Don't hesitate to comment below with any questions or share your own tips and tricks for mastering graphing lines.