Graphing Linear Equations In Slope-Intercept Form Made Easy

Quick Links :

Graphing linear equations in slope-intercept form is a fundamental concept in mathematics, and it's essential to understand it thoroughly. In this article, we'll break down the process into simple steps, making it easy for you to grasp and apply the concept.

Graphing linear equations is a crucial skill in various fields, such as physics, engineering, economics, and computer science. It helps us visualize relationships between variables, make predictions, and analyze data. However, for many students, graphing linear equations can be a daunting task, especially when dealing with slope-intercept form. But don't worry, with this article, you'll become proficient in graphing linear equations in slope-intercept form in no time.

What is Slope-Intercept Form?

Slope-intercept form is a way of writing linear equations in the format y = mx + b, where:

• m is the slope of the line
• b is the y-intercept (the point where the line intersects the y-axis)
• x is the independent variable
• y is the dependent variable

Why is Slope-Intercept Form Important?

Slope-intercept form is essential because it provides a clear and concise way to represent linear equations. It allows us to:

• Easily identify the slope and y-intercept of a line
• Write equations of lines given the slope and a point on the line
• Solve systems of linear equations
• Graph linear equations quickly and accurately

How to Graph Linear Equations in Slope-Intercept Form

Graphing linear equations in slope-intercept form is a straightforward process. Here's a step-by-step guide:

1. Write the equation in slope-intercept form (y = mx + b).
2. Identify the slope (m) and the y-intercept (b).
3. Plot the y-intercept on the coordinate plane.
4. Use the slope to find another point on the line. To do this, you can use the slope formula: m = (y2 - y1) / (x2 - x1).
5. Draw a line through the two points.

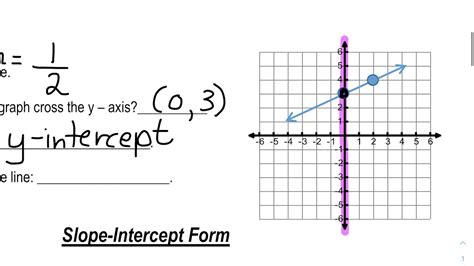
Example 1: Graphing a Linear Equation in Slope-Intercept Form

Let's graph the equation y = 2x + 3.

• Identify the slope (m = 2) and the y-intercept (b = 3).
• Plot the y-intercept (0, 3) on the coordinate plane.
• Use the slope to find another point on the line. For example, let's find the point when x = 1. Plugging in x = 1 into the equation, we get y = 2(1) + 3 = 5. So, the point is (1, 5).
• Draw a line through the two points.

Common Mistakes to Avoid When Graphing Linear Equations

When graphing linear equations, it's essential to avoid common mistakes that can lead to incorrect graphs. Here are some mistakes to watch out for:

• Not plotting the y-intercept correctly
• Not using the slope to find another point on the line
• Drawing a line that doesn't pass through the two points
• Not labeling the axes correctly

Practical Applications of Graphing Linear Equations

Graphing linear equations has numerous practical applications in various fields. Here are a few examples:

• Physics: Graphing linear equations can help us model the motion of objects, including the trajectory of projectiles and the velocity of particles.
• Economics: Graphing linear equations can help us understand the relationship between supply and demand, and make predictions about market trends.
• Computer Science: Graphing linear equations can help us develop algorithms for solving complex problems, such as finding the shortest path between two points.

Conclusion: Mastering Graphing Linear Equations

Graphing linear equations in slope-intercept form is a fundamental skill that can be mastered with practice and patience. By following the steps outlined in this article, you'll become proficient in graphing linear equations and be able to apply the concept to various fields. Remember to avoid common mistakes and take advantage of the practical applications of graphing linear equations.

Get Ready to Take Your Math Skills to the Next Level

Now that you've learned how to graph linear equations in slope-intercept form, it's time to take your math skills to the next level. Practice graphing different types of linear equations, and explore more advanced topics in mathematics. With persistence and dedication, you'll become a math master in no time.