Vector V: Component Form And Magnitude Simplified

Quick Links :

Vectors are a fundamental concept in mathematics and physics, used to represent quantities with both magnitude and direction. In this article, we will delve into the component form and magnitude of vectors, providing a comprehensive understanding of these essential concepts.

Vectors are used to describe physical quantities such as displacement, velocity, acceleration, and force. They can be represented graphically as arrows in a coordinate system, with the length of the arrow representing the magnitude of the vector and the direction of the arrow representing the direction of the vector.

Understanding the component form and magnitude of vectors is crucial in various fields, including physics, engineering, and mathematics. It allows us to analyze and solve problems involving motion, forces, and energies.

Component Form of Vectors

The component form of a vector represents the vector in terms of its components along the x, y, and z axes. It is a way of expressing a vector in a coordinate system, making it easier to work with.

A vector can be represented in component form as:

v = (v1, v2, v3)

where v1, v2, and v3 are the components of the vector along the x, y, and z axes, respectively.

For example, consider a vector v that has a magnitude of 5 units and makes an angle of 30° with the x-axis. The component form of this vector can be written as:

v = (5cos(30°), 5sin(30°), 0)

Using trigonometric functions, we can calculate the values of the components:

v = (4.33, 2.5, 0)

This represents the vector v in component form, with its components along the x, y, and z axes.

Advantages of Component Form

The component form of vectors has several advantages:

• It allows us to represent vectors in a coordinate system, making it easier to visualize and work with them.
• It enables us to perform arithmetic operations on vectors, such as addition and subtraction.
• It provides a way to express vectors in terms of their magnitude and direction.

Magnitude of Vectors

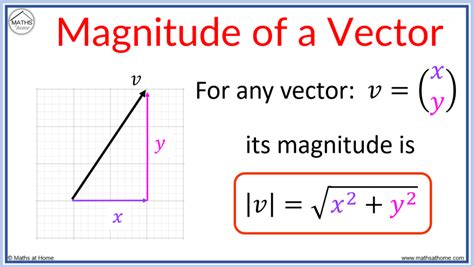
The magnitude of a vector, also known as its length or norm, is a measure of its size or amount. It is a scalar quantity, meaning it has no direction.

The magnitude of a vector can be calculated using the following formula:

|v| = √(v1^2 + v2^2 + v3^2)

where v1, v2, and v3 are the components of the vector along the x, y, and z axes, respectively.

For example, consider a vector v with components (3, 4, 0). The magnitude of this vector can be calculated as:

|v| = √(3^2 + 4^2 + 0^2) |v| = √(9 + 16) |v| = √25 |v| = 5

Therefore, the magnitude of the vector v is 5 units.

Unit Vectors

A unit vector is a vector with a magnitude of 1 unit. It is often used to represent direction, as it has no magnitude.

Unit vectors can be calculated by dividing a vector by its magnitude:

û = v / |v|

where û is the unit vector and v is the original vector.

For example, consider a vector v with components (3, 4, 0). The unit vector û can be calculated as:

û = v / |v| û = (3, 4, 0) / 5 û = (0.6, 0.8, 0)

Therefore, the unit vector û has components (0.6, 0.8, 0).

Vector Addition and Subtraction

Vectors can be added and subtracted using the component form.

Vector addition involves adding the corresponding components of two vectors:

v + w = (v1 + w1, v2 + w2, v3 + w3)

Vector subtraction involves subtracting the corresponding components of two vectors:

v - w = (v1 - w1, v2 - w2, v3 - w3)

For example, consider two vectors v and w with components (2, 3, 0) and (1, 2, 0), respectively. The sum of these vectors can be calculated as:

v + w = (2 + 1, 3 + 2, 0 + 0) v + w = (3, 5, 0)

The difference of these vectors can be calculated as:

v - w = (2 - 1, 3 - 2, 0 - 0) v - w = (1, 1, 0)

Scalar Multiplication

Scalar multiplication involves multiplying a vector by a scalar value.

Scalar multiplication changes the magnitude of the vector, but not its direction.

The product of a scalar and a vector can be calculated as:

kv = (kv1, kv2, kv3)

where k is the scalar value and v is the original vector.

For example, consider a vector v with components (2, 3, 0). The product of this vector and a scalar value k = 2 can be calculated as:

2v = (2(2), 2(3), 2(0)) 2v = (4, 6, 0)

Therefore, the product of the scalar and the vector is a new vector with components (4, 6, 0).

Vector Applications

Vectors have numerous applications in various fields, including physics, engineering, and mathematics.

Some examples of vector applications include:

• Motion: Vectors are used to describe the motion of objects, including displacement, velocity, and acceleration.
• Forces: Vectors are used to describe the forces acting on objects, including gravity, friction, and normal forces.
• Energies: Vectors are used to describe the energies of objects, including kinetic energy and potential energy.

In conclusion, understanding the component form and magnitude of vectors is essential in various fields, including physics, engineering, and mathematics. It allows us to analyze and solve problems involving motion, forces, and energies.

We hope this article has provided a comprehensive understanding of vector components and magnitude. If you have any questions or comments, please feel free to share them below.