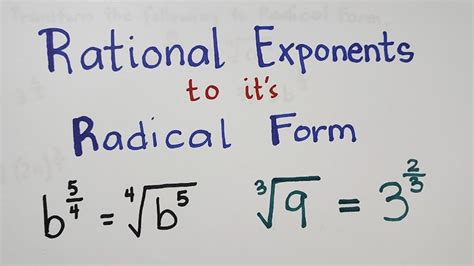Converting expressions to radical form is an essential skill in mathematics, particularly in algebra and geometry. It allows us to simplify complex expressions, solve equations, and visualize mathematical relationships. In this article, we will explore seven ways to convert expressions to radical form, providing you with a comprehensive guide to mastering this skill.
Understanding Radical Form

Before we dive into the conversion methods, let's understand what radical form means. Radical form refers to the representation of a number or expression using radicals, such as square roots, cube roots, or nth roots. This form is useful for simplifying expressions, solving equations, and graphing functions.
Method 1: Simplifying Square Roots

The first method involves simplifying square roots. To do this, we need to find the largest perfect square that divides the radicand (the number inside the square root). For example, √16 can be simplified as √(4 × 4) = √4 × √4 = 4.
Steps to Simplify Square Roots:
- Find the largest perfect square that divides the radicand.
- Write the radicand as a product of the perfect square and another factor.
- Simplify the square root by extracting the perfect square.
Method 2: Converting Rational Exponents to Radical Form

The second method involves converting rational exponents to radical form. Rational exponents are exponents that are fractions, such as 1/2, 1/3, or 2/3. To convert rational exponents to radical form, we need to rewrite the exponent as a radical using the following rule: a^(m/n) = √(a^m) / √(a^n).
Steps to Convert Rational Exponents:
- Rewrite the rational exponent as a radical using the rule a^(m/n) = √(a^m) / √(a^n).
- Simplify the radical expression by combining like terms.
Method 3: Using the Pythagorean Theorem

The third method involves using the Pythagorean theorem to convert expressions to radical form. The Pythagorean theorem states that a^2 + b^2 = c^2, where a and b are the legs of a right triangle and c is the hypotenuse. We can use this theorem to rewrite expressions involving square roots.
Steps to Use the Pythagorean Theorem:
- Identify the legs and hypotenuse of the right triangle.
- Use the Pythagorean theorem to rewrite the expression involving square roots.
Method 4: Converting Exponential Expressions

The fourth method involves converting exponential expressions to radical form. Exponential expressions involve exponents that are not fractions, such as 2^3 or 3^4. To convert exponential expressions to radical form, we need to rewrite the exponent as a radical using the following rule: a^m = √(a^(2m)).
Steps to Convert Exponential Expressions:
- Rewrite the exponential expression as a radical using the rule a^m = √(a^(2m)).
- Simplify the radical expression by combining like terms.
Method 5: Simplifying Cube Roots

The fifth method involves simplifying cube roots. To do this, we need to find the largest perfect cube that divides the radicand. For example, ∛27 can be simplified as ∛(3 × 3 × 3) = 3.
Steps to Simplify Cube Roots:
- Find the largest perfect cube that divides the radicand.
- Write the radicand as a product of the perfect cube and another factor.
- Simplify the cube root by extracting the perfect cube.
Method 6: Using Radical Conjugates

The sixth method involves using radical conjugates to convert expressions to radical form. Radical conjugates are pairs of radicals that have the same radicand but opposite signs. For example, √2 + √3 and √2 - √3 are radical conjugates.
Steps to Use Radical Conjugates:
- Identify the radical conjugates of the expression.
- Multiply the expression by the radical conjugate to eliminate the radical.
Method 7: Converting Surds to Radical Form

The seventh method involves converting surds to radical form. Surds are irrational numbers that cannot be expressed as finite decimals or fractions. To convert surds to radical form, we need to rewrite the surd as a radical using the following rule: a + √b = √(a^2 + 2ab + b).
Steps to Convert Surds:
- Rewrite the surd as a radical using the rule a + √b = √(a^2 + 2ab + b).
- Simplify the radical expression by combining like terms.
What is the difference between a radical and a surd?
+A radical is an expression involving a root, such as √2 or ∛3. A surd, on the other hand, is an irrational number that cannot be expressed as a finite decimal or fraction.
How do I simplify a cube root?
+To simplify a cube root, find the largest perfect cube that divides the radicand. Write the radicand as a product of the perfect cube and another factor. Simplify the cube root by extracting the perfect cube.
What is the Pythagorean theorem, and how is it used in radical form?
+The Pythagorean theorem states that a^2 + b^2 = c^2, where a and b are the legs of a right triangle and c is the hypotenuse. We can use this theorem to rewrite expressions involving square roots.
In conclusion, converting expressions to radical form is a valuable skill in mathematics that can help you simplify complex expressions, solve equations, and visualize mathematical relationships. By mastering the seven methods outlined in this article, you will become proficient in converting expressions to radical form and improve your overall math skills. Share your thoughts and ask questions in the comments below!