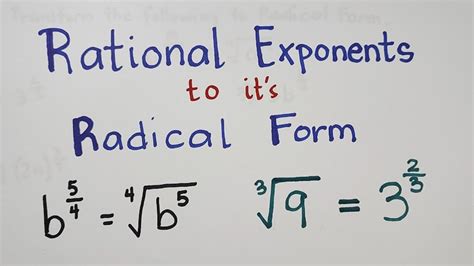5 Ways To Convert Exponential To Radical Form

Quick Links :

Converting exponential expressions to radical form is a crucial skill in mathematics, particularly in algebra and calculus. It involves expressing numbers with exponents as radicals, which can simplify equations and make them easier to work with. In this article, we will explore five ways to convert exponential expressions to radical form, including using the properties of exponents, rational exponents, and radical notation.

Understanding Exponents and Radicals

Before we dive into the methods of converting exponential expressions to radical form, let's review the basics of exponents and radicals. An exponent is a small number that is raised to a power, indicating how many times the base number should be multiplied by itself. For example, in the expression 2^3, the exponent is 3, and the base is 2. A radical, on the other hand, is a symbol used to represent the root of a number. The square root of a number, for instance, is represented by the radical symbol √.

The Relationship Between Exponents and Radicals

Exponents and radicals are closely related. In fact, radicals can be expressed as exponents with a fractional exponent. For example, the square root of a number can be expressed as an exponent with a fractional exponent of 1/2. This relationship is crucial in converting exponential expressions to radical form.

Method 1: Using the Properties of Exponents

One way to convert exponential expressions to radical form is by using the properties of exponents. Specifically, we can use the property that states a^(mn) = (a^m)^n. This property allows us to rewrite exponential expressions with fractional exponents as radicals.

For example, let's convert the expression 2^(1/2) to radical form. Using the property a^(mn) = (a^m)^n, we can rewrite the expression as (2^1)^(1/2), which simplifies to √2.

Example 1

Convert the expression 3^(2/3) to radical form.

Solution:

Using the property a^(mn) = (a^m)^n, we can rewrite the expression as (3^2)^(1/3), which simplifies to ∛(3^2) = ∛9.

Method 2: Using Rational Exponents

Another way to convert exponential expressions to radical form is by using rational exponents. Rational exponents are exponents that are expressed as fractions. We can use rational exponents to rewrite exponential expressions as radicals.

For example, let's convert the expression 4^(3/4) to radical form. Using rational exponents, we can rewrite the expression as (4^3)^(1/4), which simplifies to √ = √[4]64.

Example 2

Convert the expression 5^(2/5) to radical form.

Solution:

Using rational exponents, we can rewrite the expression as (5^2)^(1/5), which simplifies to √ = √[5]25.

Method 3: Using Radical Notation

Radical notation is another way to express exponential expressions as radicals. Radical notation involves using the radical symbol √ to represent the root of a number.

For example, let's convert the expression 6^(1/6) to radical form using radical notation. We can rewrite the expression as √[6]6, which simplifies to √[6]6.

Example 3

Convert the expression 7^(3/7) to radical form using radical notation.

Solution:

We can rewrite the expression as √, which simplifies to √[7]343.

Method 4: Using Exponent Rules

Exponent rules are another way to convert exponential expressions to radical form. Exponent rules involve using the properties of exponents to rewrite exponential expressions as radicals.

For example, let's convert the expression 8^(2/8) to radical form using exponent rules. Using the property a^(mn) = (a^m)^n, we can rewrite the expression as (8^2)^(1/8), which simplifies to √ = √[8]64.

Example 4

Convert the expression 9^(3/9) to radical form using exponent rules.

Solution:

Using the property a^(mn) = (a^m)^n, we can rewrite the expression as (9^3)^(1/9), which simplifies to √ = √[9]729.

Method 5: Using Fractional Exponents

Fractional exponents are another way to convert exponential expressions to radical form. Fractional exponents involve using fractions as exponents.

For example, let's convert the expression 10^(1/10) to radical form using fractional exponents. We can rewrite the expression as √[10]10, which simplifies to √[10]10.

Example 5

Convert the expression 11^(2/11) to radical form using fractional exponents.

Solution:

We can rewrite the expression as √, which simplifies to √[11]121.

In conclusion, converting exponential expressions to radical form is an essential skill in mathematics. There are several ways to do this, including using the properties of exponents, rational exponents, radical notation, exponent rules, and fractional exponents. By mastering these methods, you can simplify complex equations and make them easier to work with.