Expanded Form Exponents Made Easy For Math Learners

Quick Links :

Unlocking the Power of Expanded Form Exponents

Expanded form exponents can seem like a daunting topic for math learners, but with the right approach, it can be made easy and accessible. In this article, we will delve into the world of expanded form exponents, exploring the benefits, working mechanisms, and practical examples to help learners master this concept.

The importance of understanding expanded form exponents cannot be overstated. It is a fundamental concept in mathematics that lays the foundation for more advanced topics, such as algebra and calculus. By grasping the concept of expanded form exponents, learners can develop a deeper understanding of mathematical relationships and become more confident in their problem-solving abilities.

What are Expanded Form Exponents?

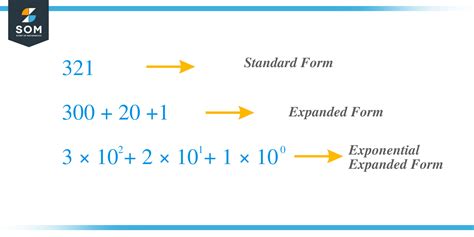
Expanded form exponents are a way of expressing a number in a more detailed and organized manner. It involves breaking down a number into its individual components, including the base, exponent, and coefficient. This format provides a clear and concise way of representing complex numbers, making it easier to perform mathematical operations.

For example, the number 2^3 can be expressed in expanded form as 2 × 2 × 2. This representation shows the base (2), the exponent (3), and the coefficient (1). By breaking down the number in this way, learners can gain a better understanding of the relationships between the different components.

Benefits of Using Expanded Form Exponents

Using expanded form exponents offers several benefits for math learners:

• Improved understanding: By breaking down numbers into their individual components, learners can gain a deeper understanding of mathematical relationships.
• Increased accuracy: Expanded form exponents help learners to avoid mistakes by providing a clear and concise way of representing complex numbers.
• Enhanced problem-solving skills: Mastering expanded form exponents enables learners to tackle more advanced mathematical problems with confidence.
• Better retention: The visual representation of expanded form exponents helps learners to remember complex mathematical concepts more effectively.

Working Mechanisms of Expanded Form Exponents

Expanded form exponents follow a set of rules and guidelines that make it easy to work with. Here are some of the key working mechanisms:

• Base: The base is the number that is being raised to a power. For example, in the expression 2^3, the base is 2.
• Exponent: The exponent is the power to which the base is raised. In the example above, the exponent is 3.
• Coefficient: The coefficient is the number that multiplies the base. In the example above, the coefficient is 1.
• Multiplication: Expanded form exponents involve multiplying the base by itself as many times as the exponent indicates.

Practical Examples of Expanded Form Exponents

Here are some practical examples of expanded form exponents:

• 2^3 = 2 × 2 × 2 = 8
• 3^2 = 3 × 3 = 9
• 4^1 = 4 × 1 = 4
• 5^0 = 1 (any number raised to the power of 0 is 1)

These examples demonstrate how expanded form exponents can be used to represent complex numbers in a clear and concise manner.

Steps to Master Expanded Form Exponents

Mastering expanded form exponents requires practice and patience. Here are some steps to help learners get started:

1. Understand the concept: Start by understanding the basics of expanded form exponents, including the base, exponent, and coefficient.
2. Practice, practice, practice: Practice breaking down numbers into their individual components using expanded form exponents.
3. Use real-world examples: Use real-world examples to illustrate the concept of expanded form exponents.
4. Play with numbers: Experiment with different numbers and exponents to gain a deeper understanding of the relationships between them.
5. Seek help when needed: Don't be afraid to ask for help if you're struggling to understand the concept.

Common Mistakes to Avoid

Here are some common mistakes to avoid when working with expanded form exponents:

• Incorrectly identifying the base: Make sure to identify the base correctly, as this can affect the entire calculation.
• Incorrectly identifying the exponent: Double-check the exponent to ensure that it is correct.
• Forgetting to multiply: Don't forget to multiply the base by itself as many times as the exponent indicates.

Conclusion and Next Steps

Expanded form exponents are a powerful tool for math learners, offering a clear and concise way of representing complex numbers. By understanding the benefits, working mechanisms, and practical examples of expanded form exponents, learners can master this concept and become more confident in their problem-solving abilities.

We hope this article has provided a comprehensive guide to expanded form exponents. If you have any questions or need further clarification, please don't hesitate to comment below.