5 Ways To Write Domain In Set Builder Form

Quick Links :

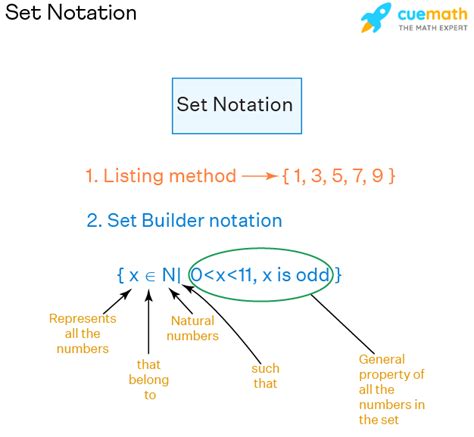
In mathematics, the set builder form is a way of describing a set using mathematical notation. It is a formal and concise way of specifying the elements of a set. Writing a domain in set builder form can be useful in various mathematical contexts, such as in defining functions, specifying the range of a function, and in set theory.

In this article, we will explore five ways to write a domain in set builder form. Before we dive into the details, let's take a moment to understand the concept of set builder form.

Understanding Set Builder Form

The set builder form is a way of describing a set using mathematical notation. It consists of two main parts: the template and the rule. The template specifies the elements of the set, while the rule specifies the conditions that these elements must satisfy.

For example, the set of all even integers can be written in set builder form as {x | x is an integer and x is even}. Here, the template is "x" and the rule is "x is an integer and x is even".

Method 1: Using Inequality

One way to write a domain in set builder form is by using inequality. For example, the domain of the function f(x) = 1 / x can be written as {x | x > 0}. Here, the template is "x" and the rule is "x > 0".

To write a domain in set builder form using inequality, follow these steps:

• Identify the variable(s) in the function or relation.
• Determine the conditions that the variable(s) must satisfy.
• Write the conditions as inequalities.
• Use the inequalities to specify the domain in set builder form.

For example, the domain of the function f(x) = 1 / (x - 2) can be written as {x | x ≠ 2}.

Example: Domain of a Rational Function

The domain of the rational function f(x) = (x + 1) / (x - 3) can be written as {x | x ≠ 3}. Here, the template is "x" and the rule is "x ≠ 3".

Method 2: Using Equalities

Another way to write a domain in set builder form is by using equalities. For example, the domain of the function f(x) = x^2 can be written as {x | x = a, where a is a real number}. Here, the template is "x" and the rule is "x = a, where a is a real number".

To write a domain in set builder form using equalities, follow these steps:

• Identify the variable(s) in the function or relation.
• Determine the conditions that the variable(s) must satisfy.
• Write the conditions as equalities.
• Use the equalities to specify the domain in set builder form.

For example, the domain of the function f(x) = x^2 + 2x + 1 can be written as {x | x = a, where a is a real number}.

Example: Domain of a Quadratic Function

The domain of the quadratic function f(x) = x^2 + 2x + 1 can be written as {x | x = a, where a is a real number}. Here, the template is "x" and the rule is "x = a, where a is a real number".

Method 3: Using Set Notation

A third way to write a domain in set builder form is by using set notation. For example, the domain of the function f(x) = 1 / x can be written as {x ∈ ℝ | x ≠ 0}. Here, the template is "x" and the rule is "x ∈ ℝ | x ≠ 0".

To write a domain in set builder form using set notation, follow these steps:

• Identify the variable(s) in the function or relation.
• Determine the conditions that the variable(s) must satisfy.
• Write the conditions using set notation.
• Use the set notation to specify the domain in set builder form.

For example, the domain of the function f(x) = x^2 can be written as {x ∈ ℝ | x = a, where a is a real number}.

Example: Domain of a Polynomial Function

The domain of the polynomial function f(x) = x^3 + 2x^2 + x + 1 can be written as {x ∈ ℝ | x = a, where a is a real number}. Here, the template is "x" and the rule is "x ∈ ℝ | x = a, where a is a real number".

Method 4: Using Interval Notation

A fourth way to write a domain in set builder form is by using interval notation. For example, the domain of the function f(x) = 1 / x can be written as (0, ∞) ∪ (-∞, 0). Here, the template is "x" and the rule is "x ∈ (0, ∞) ∪ (-∞, 0)".

To write a domain in set builder form using interval notation, follow these steps:

• Identify the variable(s) in the function or relation.
• Determine the conditions that the variable(s) must satisfy.
• Write the conditions using interval notation.
• Use the interval notation to specify the domain in set builder form.

For example, the domain of the function f(x) = x^2 can be written as (-∞, ∞).

Example: Domain of a Rational Function

The domain of the rational function f(x) = (x + 1) / (x - 3) can be written as (-∞, 3) ∪ (3, ∞). Here, the template is "x" and the rule is "x ∈ (-∞, 3) ∪ (3, ∞)".

Method 5: Using Combination of Methods

A fifth way to write a domain in set builder form is by using a combination of methods. For example, the domain of the function f(x) = 1 / (x^2 + 1) can be written as {x ∈ ℝ | x^2 + 1 ≠ 0} or (-∞, ∞). Here, the template is "x" and the rule is "x ∈ ℝ | x^2 + 1 ≠ 0" or "x ∈ (-∞, ∞)".

To write a domain in set builder form using a combination of methods, follow these steps:

• Identify the variable(s) in the function or relation.
• Determine the conditions that the variable(s) must satisfy.
• Write the conditions using a combination of methods.
• Use the combination of methods to specify the domain in set builder form.

For example, the domain of the function f(x) = x^3 + 2x^2 + x + 1 can be written as {x ∈ ℝ | x = a, where a is a real number} or (-∞, ∞).

Example: Domain of a Polynomial Function

The domain of the polynomial function f(x) = x^3 + 2x^2 + x + 1 can be written as {x ∈ ℝ | x = a, where a is a real number} or (-∞, ∞). Here, the template is "x" and the rule is "x ∈ ℝ | x = a, where a is a real number" or "x ∈ (-∞, ∞)".

In conclusion, there are several ways to write a domain in set builder form, including using inequality, equality, set notation, interval notation, and a combination of methods. By following the steps outlined in this article, you can write a domain in set builder form using the method that best suits your needs.

We hope this article has been helpful in explaining the different ways to write a domain in set builder form. If you have any further questions or would like to share your thoughts, please leave a comment below.