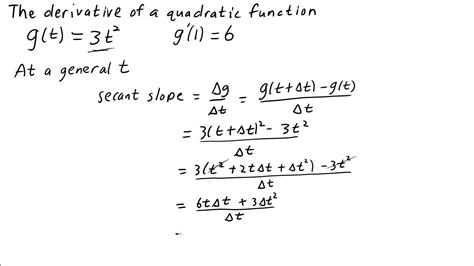Understanding the Derivative of Quadratic Forms

Quadratic forms are a fundamental concept in mathematics, particularly in algebra and calculus. They are used to describe the relationship between variables and are commonly used in physics, engineering, and economics. One of the crucial aspects of quadratic forms is finding their derivatives. In this article, we will explore three ways to find the derivative of a quadratic form.
Quadratic forms are expressions of the form ax^2 + bx + c, where a, b, and c are constants, and x is the variable. The derivative of a quadratic form is a linear function that represents the rate of change of the quadratic form with respect to the variable. Finding the derivative of a quadratic form is essential in many applications, such as optimization problems, physics, and engineering.
Method 1: Using the Power Rule

One of the simplest ways to find the derivative of a quadratic form is by using the power rule. The power rule states that if f(x) = x^n, then f'(x) = nx^(n-1). This rule can be applied to quadratic forms by differentiating each term separately.
For example, consider the quadratic form f(x) = 3x^2 + 2x + 1. To find the derivative, we can apply the power rule to each term:
f'(x) = d(3x^2)/dx + d(2x)/dx + d(1)/dx = 6x + 2
This shows that the derivative of the quadratic form f(x) = 3x^2 + 2x + 1 is f'(x) = 6x + 2.
Advantages of Using the Power Rule
The power rule is a simple and straightforward method for finding the derivative of a quadratic form. It is easy to apply and requires minimal calculations. Additionally, the power rule can be used to find the derivative of any polynomial function, making it a versatile tool in calculus.
Disadvantages of Using the Power Rule
One of the limitations of the power rule is that it can only be used for polynomial functions. If the quadratic form contains non-polynomial terms, such as trigonometric or exponential functions, the power rule cannot be applied.
Method 2: Using the Product Rule

Another way to find the derivative of a quadratic form is by using the product rule. The product rule states that if f(x) = u(x)v(x), then f'(x) = u'(x)v(x) + u(x)v'(x).
For example, consider the quadratic form f(x) = x^2 + 2x. To find the derivative, we can rewrite the quadratic form as f(x) = x(x + 2) and apply the product rule:
f'(x) = d(x)/dx(x + 2) + x d(x + 2)/dx = (x + 2) + x(1) = 2x + 2
This shows that the derivative of the quadratic form f(x) = x^2 + 2x is f'(x) = 2x + 2.
Advantages of Using the Product Rule
The product rule is a powerful tool for finding the derivative of quadratic forms, especially when the quadratic form can be rewritten as a product of two functions. It is also useful for finding the derivative of non-polynomial functions.
Disadvantages of Using the Product Rule
One of the limitations of the product rule is that it can be more complicated to apply than the power rule. Additionally, the product rule requires the quadratic form to be rewritten as a product of two functions, which may not always be possible.
Method 3: Using Implicit Differentiation

Implicit differentiation is another method for finding the derivative of a quadratic form. Implicit differentiation involves differentiating both sides of an equation with respect to the variable.
For example, consider the quadratic form f(x) = x^2 + 2x. To find the derivative, we can differentiate both sides of the equation with respect to x:
d(x^2 + 2x)/dx = d(f(x))/dx 2x + 2 = f'(x)
This shows that the derivative of the quadratic form f(x) = x^2 + 2x is f'(x) = 2x + 2.
Advantages of Using Implicit Differentiation
Implicit differentiation is a versatile method for finding the derivative of quadratic forms, especially when the quadratic form is given as an equation. It is also useful for finding the derivative of non-polynomial functions.
Disadvantages of Using Implicit Differentiation
One of the limitations of implicit differentiation is that it can be more complicated to apply than the power rule and the product rule. Additionally, implicit differentiation requires the quadratic form to be given as an equation, which may not always be the case.
In conclusion, there are three ways to find the derivative of a quadratic form: using the power rule, using the product rule, and using implicit differentiation. Each method has its advantages and disadvantages, and the choice of method depends on the specific quadratic form and the context of the problem.
What is a quadratic form?
+A quadratic form is an expression of the form ax^2 + bx + c, where a, b, and c are constants, and x is the variable.
Why is it important to find the derivative of a quadratic form?
+Finding the derivative of a quadratic form is essential in many applications, such as optimization problems, physics, and engineering, as it represents the rate of change of the quadratic form with respect to the variable.
What are the advantages and disadvantages of using the power rule to find the derivative of a quadratic form?
+The power rule is a simple and straightforward method for finding the derivative of a quadratic form, but it can only be used for polynomial functions and may not be applicable for non-polynomial terms.