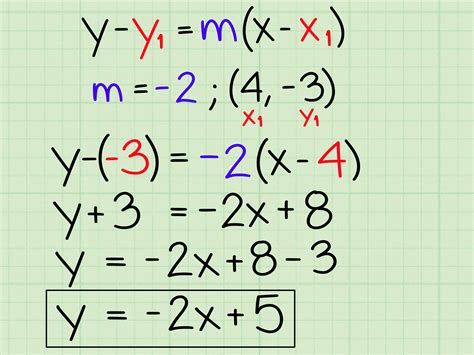Convert To Slope Intercept Form Made Easy

Quick Links :

Converting equations to slope-intercept form is a fundamental concept in algebra, and it's essential to understand it to succeed in math and science. Slope-intercept form is a way of expressing linear equations in a simple and intuitive way, making it easier to analyze and solve problems.

What is Slope-Intercept Form?

Slope-intercept form is a linear equation written in the form y = mx + b, where:

• m is the slope of the line, which represents the rate of change between the x and y variables.
• b is the y-intercept, which is the point where the line intersects the y-axis.

Why is Slope-Intercept Form Important?

Slope-intercept form is essential in various mathematical and real-world applications. It helps us:

• Understand the relationship between variables and how they change.
• Analyze and interpret data in graphs and tables.
• Solve linear equations and systems of equations.
• Model real-world phenomena, such as population growth, financial transactions, and physics problems.

How to Convert to Slope-Intercept Form

Converting equations to slope-intercept form involves rearranging the terms to isolate y on one side of the equation. Here are the steps:

1. Start with a linear equation: Begin with a linear equation in any form, such as standard form (ax + by = c) or point-slope form (y - y1 = m(x - x1)).
2. Isolate y: Rearrange the equation to isolate y on one side. This may involve adding, subtracting, multiplying, or dividing both sides of the equation by the same value.
3. Simplify: Simplify the equation by combining like terms and removing any unnecessary parentheses or brackets.

Examples of Converting to Slope-Intercept Form

Let's consider some examples:

• Example 1: Convert the equation 2x + 3y = 5 to slope-intercept form.

2x + 3y = 5 3y = -2x + 5 y = (-2/3)x + 5/3

• Example 2: Convert the equation x - 2y = 3 to slope-intercept form.

x - 2y = 3 -2y = -x + 3 y = (1/2)x - 3/2

Tips and Tricks for Converting to Slope-Intercept Form

Here are some tips and tricks to help you convert equations to slope-intercept form:

• Check your work: Always check your work by plugging the original equation back into the converted equation to ensure it's true.
• Use online tools: Utilize online tools, such as equation solvers or graphing calculators, to help you convert equations and check your work.
• Practice, practice, practice: The more you practice converting equations to slope-intercept form, the more comfortable you'll become with the process.

Common Mistakes to Avoid

When converting equations to slope-intercept form, be careful to avoid these common mistakes:

• Incorrectly isolating y: Make sure to isolate y on one side of the equation, rather than x or another variable.
• Forgetting to simplify: Simplify the equation by combining like terms and removing unnecessary parentheses or brackets.
• Rounding errors: Be mindful of rounding errors when converting equations, especially when working with decimals or fractions.

Real-World Applications of Slope-Intercept Form

Slope-intercept form has numerous real-world applications, including:

• Finance: Understanding the slope-intercept form of linear equations helps you analyze financial transactions, such as interest rates and investment returns.
• Science: Slope-intercept form is used to model population growth, chemical reactions, and physics problems, such as motion and gravity.
• Engineering: Engineers use slope-intercept form to design and optimize systems, such as bridges, buildings, and electronic circuits.

Conclusion: Mastering Slope-Intercept Form

Converting equations to slope-intercept form is a crucial skill in algebra and mathematics. By following the steps and tips outlined in this article, you'll become proficient in converting equations to slope-intercept form. Remember to practice regularly and apply your knowledge to real-world problems to reinforce your understanding.