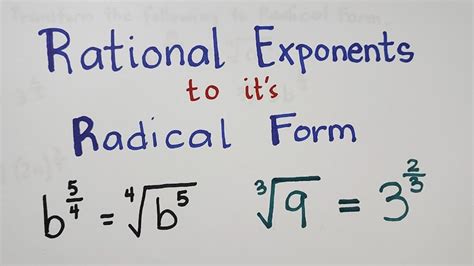Converting Radicals To Exponential Form Made Easy

Quick Links :

Converting Radicals To Exponential Form Made Easy

Are you struggling to convert radicals to exponential form? You're not alone! Many students find this concept challenging, but with the right approach, it can be made easy. In this article, we'll explore the basics of radicals and exponential form, and provide step-by-step instructions on how to convert radicals to exponential form.

Radicals are mathematical expressions that involve the square root or other roots of a number. They are commonly used in algebra, geometry, and other branches of mathematics. Exponential form, on the other hand, is a way of expressing numbers using exponents. It's a more compact and convenient way of writing numbers, especially when dealing with large or complex expressions.

Why Convert Radicals to Exponential Form?

Converting radicals to exponential form is important for several reasons. Firstly, it allows us to simplify complex expressions and make them easier to work with. Secondly, it enables us to compare and contrast different expressions, which is crucial in algebra and other areas of mathematics. Finally, exponential form is often required in mathematical proofs and theorems, making it an essential skill for math enthusiasts.

Understanding Radicals

Before we dive into converting radicals to exponential form, it's essential to understand the basics of radicals. A radical is a mathematical expression that involves the square root or other roots of a number. The most common type of radical is the square root, denoted by the symbol √. Other types of radicals include the cube root (∛), fourth root (∜), and so on.

Radicals can be classified into two main categories: simple radicals and complex radicals. Simple radicals involve the square root or other roots of a single number, whereas complex radicals involve multiple numbers or variables.

Simple Radicals

Simple radicals are the easiest type of radical to work with. They involve the square root or other roots of a single number. For example:

√16 = 4 ∛27 = 3 ∜256 = 4

In each of these examples, we're finding the square root or other roots of a single number.

Complex Radicals

Complex radicals involve multiple numbers or variables. They can be more challenging to work with, but they're still essential in mathematics. For example:

√(x + 3) =? ∛(2x - 5) =?

In these examples, we're finding the square root or other roots of an expression that involves multiple numbers or variables.

Converting Radicals to Exponential Form

Now that we've covered the basics of radicals, let's explore how to convert them to exponential form. The process is relatively straightforward and involves using the following formula:

a^(1/n) = nth root of a

In this formula, a is the number or expression inside the radical, and n is the index of the radical. For example:

√a = a^(1/2) ∛a = a^(1/3) ∜a = a^(1/4)

Using this formula, we can convert simple radicals to exponential form:

√16 = 16^(1/2) = 4 ∛27 = 27^(1/3) = 3 ∜256 = 256^(1/4) = 4

Converting complex radicals to exponential form is slightly more challenging, but it still involves using the same formula:

√(x + 3) = (x + 3)^(1/2) ∛(2x - 5) = (2x - 5)^(1/3)

Step-by-Step Instructions

Here are the step-by-step instructions for converting radicals to exponential form:

1. Identify the type of radical you're working with (simple or complex).
2. Identify the number or expression inside the radical.
3. Identify the index of the radical (n).
4. Use the formula a^(1/n) to convert the radical to exponential form.

Examples and Applications

Let's explore some examples and applications of converting radicals to exponential form:

• Simplifying complex expressions: Converting radicals to exponential form can help simplify complex expressions and make them easier to work with.
• Comparing and contrasting expressions: Exponential form allows us to compare and contrast different expressions, which is crucial in algebra and other areas of mathematics.
• Mathematical proofs and theorems: Exponential form is often required in mathematical proofs and theorems, making it an essential skill for math enthusiasts.

Real-World Applications

Converting radicals to exponential form has numerous real-world applications, including:

• Physics and engineering: Radicals and exponential form are used extensively in physics and engineering to model complex phenomena and solve problems.
• Computer science: Radicals and exponential form are used in computer science to develop algorithms and solve complex problems.
• Economics: Radicals and exponential form are used in economics to model economic systems and solve problems.

Conclusion

Converting radicals to exponential form is a crucial skill in mathematics, with numerous applications in physics, engineering, computer science, and economics. By understanding the basics of radicals and using the formula a^(1/n), we can convert simple and complex radicals to exponential form. Remember to identify the type of radical, the number or expression inside the radical, and the index of the radical, and use the formula to convert the radical to exponential form.

We hope this article has helped you understand the concept of converting radicals to exponential form. If you have any questions or comments, please don't hesitate to ask.