5 Easy Steps To Convert Complex Numbers To Polar Form

Quick Links :

Hide

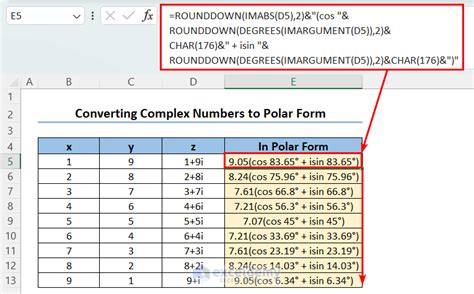
Representing complex numbers in polar form is a fundamental concept in mathematics and engineering, offering a more intuitive and convenient way to analyze and manipulate these numbers. The polar form of a complex number, also known as trigonometric form, is a way to express a complex number in terms of its magnitude (or length) and angle. This form is extremely useful in various applications, including signal processing, control systems, and electronics. Here, we will delve into the simple steps to convert complex numbers to polar form, making it easy for anyone to grasp this essential mathematical concept.

Understanding Complex Numbers

Before diving into the conversion process, it's crucial to understand what complex numbers are. A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit, satisfying the equation i^2 = -1. In this form, 'a' is known as the real part, and 'bi' is known as the imaginary part.

The Importance of Polar Form

The polar form of a complex number offers several advantages over the Cartesian form. It simplifies the process of multiplication and division of complex numbers, making it easier to perform operations in many practical applications. Moreover, the polar form provides a clear geometric interpretation, making it easier to visualize and understand complex number operations.

Step 1: Understand the Cartesian Form

The first step in converting a complex number to polar form is to ensure you understand the complex number in its Cartesian form, which is a + bi. Here, 'a' represents the real part, and 'bi' represents the imaginary part.

Example:

Consider the complex number 3 + 4i. In this case, a = 3 (the real part), and b = 4 (the coefficient of the imaginary part).

Step 2: Calculate the Magnitude

The magnitude (or modulus) of a complex number is the distance from the origin (0,0) to the point representing the complex number in the complex plane. It is calculated using the formula: r = √(a^2 + b^2).

Example (Continued):

For the complex number 3 + 4i, the magnitude r = √(3^2 + 4^2) = √(9 + 16) = √25 = 5.

Step 3: Calculate the Angle (Argument)

The angle, or argument, is the angle between the positive real axis and the line connecting the origin to the complex number. It can be calculated using the formula: θ = arctan(b/a).

Example (Continued):

For the complex number 3 + 4i, the angle θ = arctan(4/3). Using a calculator, we find θ ≈ 53.13 degrees. However, angles are usually expressed in radians in mathematical and engineering applications, so θ ≈ 0.927 radians.

Step 4: Express in Polar Form

With the magnitude (r) and angle (θ) calculated, the complex number can now be expressed in polar form as: r(cos(θ) + i sin(θ)).

Example (Continued):

The complex number 3 + 4i can be expressed in polar form as 5(cos(0.927) + i sin(0.927)).

Step 5: Simplify if Necessary

In some cases, the polar form expression might be simplified further, depending on the specific values of r and θ. However, this step is not always necessary and depends on the context in which the polar form is being used.

In conclusion, converting a complex number to polar form is a straightforward process that involves calculating the magnitude and angle, then expressing the number in terms of these two components. This process not only simplifies many mathematical operations involving complex numbers but also provides a deeper geometric understanding of complex number properties and behaviors.

If you found this guide helpful in understanding how to convert complex numbers to polar form, we invite you to share your thoughts or questions in the comments below. Your feedback is invaluable in helping us create more informative content for our readers.