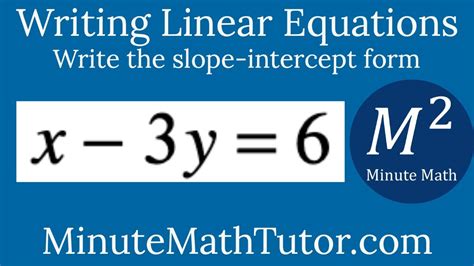Converting X 3y 6 To Slope Intercept Form Easily

Quick Links :

In mathematics, equations are used to describe relationships between variables. One of the most common forms of linear equations is the slope-intercept form, which is expressed as y = mx + b. Here, m represents the slope of the line, and b is the y-intercept.

Equations can be given in various forms, including standard form, point-slope form, and slope-intercept form. When we are given an equation in a different form, it's essential to convert it to the slope-intercept form to easily identify the slope and y-intercept.

In this article, we'll learn how to convert an equation from standard form to slope-intercept form, focusing on the equation X 3y 6. We'll explore the steps involved in the conversion process, the benefits of using slope-intercept form, and provide examples to illustrate the concept.

Understanding Standard Form and Slope-Intercept Form

Standard form is a way of expressing linear equations, where the equation is written in the form Ax + By = C. Here, A, B, and C are constants, and x and y are variables.

On the other hand, slope-intercept form is another way of expressing linear equations, which is written as y = mx + b. Here, m is the slope of the line, and b is the y-intercept.

Benefits of Slope-Intercept Form

The slope-intercept form has several benefits that make it a popular choice for expressing linear equations. Some of the advantages of slope-intercept form include:

• Easy identification of the slope and y-intercept
• Simple to graph the equation
• Convenient for solving systems of equations
• Useful for real-world applications, such as physics and engineering

Converting X 3y 6 to Slope-Intercept Form

To convert the equation X 3y 6 to slope-intercept form, we need to isolate the variable y. Here are the steps:

1. Rearrange the equation to isolate y: X - 6 = 3y
2. Divide both sides by 3: (X - 6) / 3 = y
3. Simplify the equation: y = (X / 3) - 2

Example 1: Graphing the Equation

Now that we have the equation in slope-intercept form, we can graph it. To graph the equation, we need to plot two points and draw a line through them. We can choose any two values of x to find the corresponding values of y.

For example, let's choose x = 0 and x = 3.

When x = 0: y = (0 / 3) - 2 y = -2

When x = 3: y = (3 / 3) - 2 y = 1 - 2 y = -1

Plotting these points on a coordinate plane and drawing a line through them gives us the graph of the equation.

Practical Applications of Slope-Intercept Form

Slope-intercept form has several practical applications in real-world scenarios. Some of the examples include:

• Physics: Slope-intercept form is used to describe the motion of objects under the influence of gravity or other forces.
• Engineering: Slope-intercept form is used to design and analyze systems, such as bridges and buildings.
• Economics: Slope-intercept form is used to model economic systems, such as supply and demand curves.

Example 2: Real-World Application

A company is producing a new product, and the cost of production is directly proportional to the number of units produced. The cost of producing 100 units is $1000, and the cost of producing 200 units is $1500.

Let's use the slope-intercept form to model the cost of production.

Let C be the cost of production and x be the number of units produced.

We can write the equation in slope-intercept form as: C = mx + b

We are given two points on the graph: (100, 1000) and (200, 1500).

Using the slope formula, we can find the slope: m = (1500 - 1000) / (200 - 100) m = 500 / 100 m = 5

Now that we have the slope, we can find the y-intercept: 1000 = 5(100) + b 1000 = 500 + b b = 500

So, the equation in slope-intercept form is: C = 5x + 500

This equation can be used to predict the cost of production for any number of units.

Conclusion and Final Thoughts

Converting an equation from standard form to slope-intercept form is a straightforward process that involves isolating the variable y. By following the steps outlined in this article, you can easily convert any equation to slope-intercept form.

Slope-intercept form has several benefits, including easy identification of the slope and y-intercept, simple graphing, and convenience for solving systems of equations.

In conclusion, slope-intercept form is a powerful tool for analyzing and solving linear equations. By mastering the conversion process, you can unlock the full potential of slope-intercept form and apply it to a wide range of real-world problems.

We hope this article has provided you with a comprehensive understanding of converting X 3y 6 to slope-intercept form. If you have any questions or need further clarification, please don't hesitate to ask.