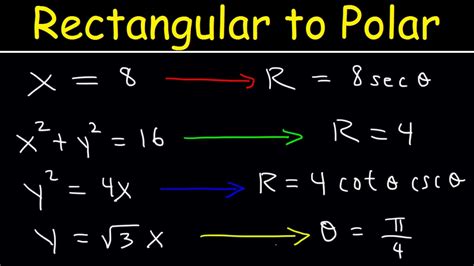Convert Rectangular To Polar Equation Easily

Quick Links :

Converting rectangular equations to polar equations is a fundamental concept in mathematics, particularly in the fields of algebra and trigonometry. Rectangular equations, also known as Cartesian equations, represent the relationship between two variables, x and y, in a coordinate plane. On the other hand, polar equations represent the relationship between a point and the origin in a polar coordinate system.

In this article, we will delve into the process of converting rectangular equations to polar equations, explore the benefits of doing so, and provide practical examples to illustrate the concept.

Understanding Rectangular and Polar Coordinate Systems

Before we dive into the conversion process, let's briefly review the basics of rectangular and polar coordinate systems.

In a rectangular coordinate system, a point is represented by an ordered pair (x, y), where x is the horizontal distance from the origin and y is the vertical distance. In contrast, a polar coordinate system represents a point by its distance from the origin (r) and the angle between the positive x-axis and the line connecting the origin to the point (θ).

Benefits of Converting Rectangular to Polar Equations

Converting rectangular equations to polar equations offers several benefits:

• Simplified equations: Polar equations can be more straightforward and easier to work with, especially when dealing with circular or periodic functions.
• Visual representation: Polar equations provide a clearer visual representation of the relationship between variables, making it easier to understand and analyze complex relationships.
• Easier calculations: Polar equations can simplify calculations, especially when working with trigonometric functions.

Steps to Convert Rectangular to Polar Equations

Converting rectangular equations to polar equations involves a few simple steps:

1. Replace x and y with r and θ: In the rectangular equation, replace x with rcos(θ) and y with rsin(θ).
2. Simplify the equation: Simplify the resulting equation by combining like terms and canceling out any common factors.
3. Express the equation in terms of r and θ: Rearrange the equation to express it solely in terms of r and θ.

Examples of Converting Rectangular to Polar Equations

Let's consider a few examples to illustrate the conversion process:

Example 1: Converting a Simple Rectangular Equation

Rectangular equation: x^2 + y^2 = 4

1. Replace x and y with r and θ: (rcos(θ))^2 + (rsin(θ))^2 = 4
2. Simplify the equation: r^2(cos^2(θ) + sin^2(θ)) = 4
3. Express the equation in terms of r and θ: r^2 = 4

Polar equation: r = 2

Example 2: Converting a Trigonometric Rectangular Equation

Rectangular equation: y = sin(x)

1. Replace x and y with r and θ: rsin(θ) = sin(rcos(θ))
2. Simplify the equation: rsin(θ) = sin(r cos(θ))
3. Express the equation in terms of r and θ: θ = rcos(θ)

Polar equation: θ = rcos(θ)

Tips and Tricks for Converting Rectangular to Polar Equations

When converting rectangular equations to polar equations, keep the following tips and tricks in mind:

• Use trigonometric identities to simplify the equation.
• Express the equation in terms of r and θ to ensure it is in polar form.
• Check the equation for any restrictions on r and θ.

Common Mistakes to Avoid

When converting rectangular equations to polar equations, be sure to avoid the following common mistakes:

• Forgetting to replace x and y with r and θ.
• Not simplifying the equation correctly.
• Not expressing the equation in terms of r and θ.

Conclusion

Converting rectangular equations to polar equations is a valuable skill in mathematics, offering a range of benefits from simplified equations to easier calculations. By following the steps outlined in this article and practicing with examples, you can become proficient in converting rectangular equations to polar equations.