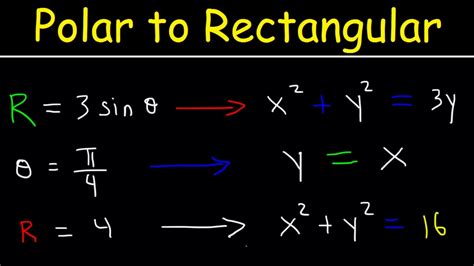Convert Polar Equations To Rectangular Form Easily

Quick Links :

Converting polar equations to rectangular form is a fundamental concept in mathematics, particularly in trigonometry and calculus. Polar equations are often used to describe curves and shapes in a two-dimensional plane, but they can be difficult to work with in certain situations. Rectangular form, on the other hand, is a more intuitive and familiar way of representing equations, making it easier to visualize and manipulate the resulting graphs. In this article, we will explore the process of converting polar equations to rectangular form, including the benefits, working mechanisms, and practical examples.

Understanding Polar Equations

Polar equations are equations that describe a relationship between the distance from a point (the origin) and the angle formed by a line connecting the point to the origin. These equations are typically written in the form r = f(θ), where r is the distance from the origin and θ is the angle formed by the line. Polar equations can be used to describe a wide range of curves and shapes, including circles, spirals, and cardioids.

The Benefits of Converting to Rectangular Form

Converting polar equations to rectangular form has several benefits. Firstly, rectangular form is often more intuitive and easier to visualize than polar form. This makes it easier to understand the behavior of the curve or shape described by the equation. Secondly, rectangular form is more amenable to manipulation and transformation, making it easier to perform tasks such as finding the derivative or integral of the equation. Finally, rectangular form is often more convenient for graphing and plotting, as most graphing software and calculators are designed to work with rectangular coordinates.

The Working Mechanisms of Converting Polar Equations

Converting polar equations to rectangular form involves using the relationships between polar and rectangular coordinates. The most common conversion formulas are:

• x = r cos(θ)
• y = r sin(θ)

These formulas can be used to convert a polar equation r = f(θ) into a rectangular equation y = f(x). The process typically involves substituting the expression for r into the conversion formulas and simplifying the resulting equation.

Step-by-Step Guide to Converting Polar Equations

Converting polar equations to rectangular form can be a straightforward process if you follow the steps below:

1. Identify the polar equation: Start by identifying the polar equation you want to convert. Make sure it is in the form r = f(θ).
2. Apply the conversion formulas: Use the conversion formulas x = r cos(θ) and y = r sin(θ) to substitute the expression for r into the polar equation.
3. Simplify the resulting equation: Simplify the resulting equation to obtain a rectangular equation in the form y = f(x).
4. Rearrange the equation (optional): If necessary, rearrange the equation to isolate y on one side of the equation.

Example: Converting a Polar Equation to Rectangular Form

Suppose we want to convert the polar equation r = 2 cos(θ) to rectangular form. We can follow the steps above to obtain:

• x = r cos(θ) = 2 cos(θ) cos(θ) = 2 cos^2(θ)
• y = r sin(θ) = 2 cos(θ) sin(θ) = 2 cos(θ) sin(θ)

Simplifying the resulting equation, we get:

• x = 2 cos^2(θ)
• y = 2 cos(θ) sin(θ)

Rearranging the equation to isolate y, we get:

• y = 2x sin(θ)

This is the rectangular form of the original polar equation.

Practical Applications of Converting Polar Equations

Converting polar equations to rectangular form has numerous practical applications in various fields, including:

• Engineering: Converting polar equations to rectangular form is crucial in engineering design, particularly in the design of curves and shapes for structures and mechanisms.
• Physics: Polar equations are often used to describe the motion of objects in physics, and converting them to rectangular form can help in understanding and analyzing the motion.
• Computer Science: Converting polar equations to rectangular form is essential in computer graphics and game development, where curves and shapes need to be rendered and manipulated.

Common Challenges and Solutions

Converting polar equations to rectangular form can be challenging, especially when dealing with complex equations. Some common challenges and solutions include:

• Simplifying the resulting equation: Use algebraic manipulation and trigonometric identities to simplify the resulting equation.
• Dealing with multiple solutions: Be aware of multiple solutions and use trigonometric identities to eliminate them.
• Graphing the resulting equation: Use graphing software or calculators to visualize the resulting equation and check for any errors.

Conclusion and Final Thoughts

Converting polar equations to rectangular form is a fundamental concept in mathematics and has numerous practical applications. By following the steps outlined above and using the conversion formulas, you can easily convert polar equations to rectangular form. Remember to simplify the resulting equation, deal with multiple solutions, and graph the resulting equation to ensure accuracy. With practice and experience, you will become proficient in converting polar equations to rectangular form, opening up new possibilities for solving complex problems and analyzing curves and shapes.

What's Next?

We hope this article has helped you understand the process of converting polar equations to rectangular form. If you have any questions or need further clarification, please don't hesitate to comment below. Share this article with your friends and colleagues who may benefit from learning about this topic. Happy math-ing!