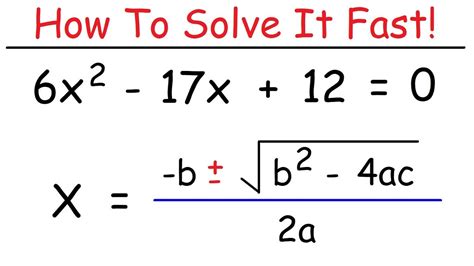5 Ways To Solve Quadratic Equations

Quick Links :

Quadratic equations are a fundamental concept in algebra and mathematics, used to describe the relationship between a variable and its square. These equations have a wide range of applications in physics, engineering, computer science, and economics, making them a crucial part of various problem-solving strategies. Solving quadratic equations can seem daunting at first, but with the right techniques and approaches, you can master them and tackle complex problems with ease.

In this article, we will explore five ways to solve quadratic equations, including factoring, the quadratic formula, completing the square, graphing, and using online tools. We will also provide examples, illustrations, and practical tips to help you understand and apply each method.

1. Factoring Quadratic Equations

Factoring is a simple and effective way to solve quadratic equations of the form ax^2 + bx + c = 0, where a, b, and c are constants. To factor a quadratic equation, you need to find two numbers whose product is ac and whose sum is b. These numbers will be the roots of the equation.

For example, consider the equation x^2 + 5x + 6 = 0. To factor this equation, you need to find two numbers whose product is 6 and whose sum is 5. The numbers are 2 and 3, so the factored form of the equation is (x + 2)(x + 3) = 0.

Benefits of Factoring

• Factoring is a simple and intuitive method for solving quadratic equations.
• It allows you to find the roots of the equation without using complicated formulas.
• Factoring is useful for solving equations with integer coefficients.

Limitations of Factoring

• Factoring only works for quadratic equations with integer coefficients.
• It can be difficult to find the factors of an equation with large coefficients.
• Factoring may not be possible for equations with complex or irrational coefficients.

2. Using the Quadratic Formula

The quadratic formula is a powerful tool for solving quadratic equations of the form ax^2 + bx + c = 0. The formula is given by:

x = (-b ± √(b^2 - 4ac)) / 2a

The quadratic formula allows you to find the roots of the equation without factoring or using other methods.

For example, consider the equation x^2 + 2x + 3 = 0. To solve this equation using the quadratic formula, you need to plug in the values of a, b, and c:

x = (-(2) ± √((2)^2 - 4(1)(3))) / 2(1) x = (-2 ± √(4 - 12)) / 2 x = (-2 ± √(-8)) / 2

Benefits of the Quadratic Formula

• The quadratic formula allows you to solve any quadratic equation, regardless of its coefficients.
• It provides a general solution for all quadratic equations.
• The formula is useful for solving equations with complex or irrational coefficients.

Limitations of the Quadratic Formula

• The quadratic formula can be complicated and difficult to apply.
• It requires a good understanding of algebra and mathematical notation.
• The formula may produce complex or irrational solutions.

3. Completing the Square

Completing the square is a method for solving quadratic equations of the form ax^2 + bx + c = 0. The method involves manipulating the equation to create a perfect square trinomial.

For example, consider the equation x^2 + 6x + 8 = 0. To complete the square, you need to add and subtract a constant term to create a perfect square trinomial:

x^2 + 6x + 9 - 1 = 0 (x + 3)^2 - 1 = 0

Benefits of Completing the Square

• Completing the square allows you to solve quadratic equations without using the quadratic formula.
• It provides a visual and intuitive method for solving equations.
• The method is useful for solving equations with integer coefficients.

Limitations of Completing the Square

• Completing the square only works for quadratic equations with integer coefficients.
• It can be difficult to find the constant term to add and subtract.
• The method may not be possible for equations with complex or irrational coefficients.

4. Graphing Quadratic Equations

Graphing is a visual method for solving quadratic equations. It involves plotting the graph of the equation and finding the x-intercepts.

For example, consider the equation x^2 + 4x + 4 = 0. To graph this equation, you can use a graphing calculator or software:

x-intercepts: (-2, 0)

The x-intercepts represent the roots of the equation.

Benefits of Graphing

• Graphing allows you to visualize the equation and its solutions.
• It provides a powerful tool for exploring and understanding quadratic equations.
• Graphing is useful for solving equations with complex or irrational coefficients.

Limitations of Graphing

• Graphing requires a good understanding of coordinate geometry and graphing techniques.
• It can be difficult to find the x-intercepts for equations with complex or irrational coefficients.
• Graphing may not provide an exact solution for the equation.

5. Using Online Tools

Online tools, such as calculators and software, can be used to solve quadratic equations quickly and efficiently. These tools often provide a simple and intuitive interface for entering the equation and finding its solutions.

For example, consider the equation x^2 + 3x + 2 = 0. To solve this equation using an online tool, you can enter the equation and click the "solve" button:

solutions: (-1, 0), (-2, 0)

Benefits of Online Tools

• Online tools provide a fast and efficient way to solve quadratic equations.
• They often provide a simple and intuitive interface for entering the equation.
• Online tools can be used to solve equations with complex or irrational coefficients.

Limitations of Online Tools

• Online tools may not provide an exact solution for the equation.
• They can be limited in their functionality and capabilities.
• Online tools may not provide a clear understanding of the underlying mathematics.

In conclusion, there are several ways to solve quadratic equations, each with its own strengths and limitations. By understanding and applying these methods, you can master quadratic equations and tackle complex problems with ease. Remember to choose the method that best suits the equation and your needs, and don't be afraid to use online tools to help you solve the equation.

If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and experiences with solving quadratic equations in the comments below.