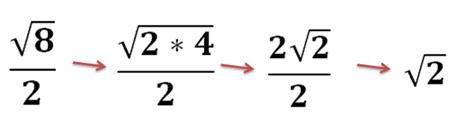
Radical form simplified is a crucial concept in mathematics, particularly in algebra and geometry. It enables us to simplify complex expressions and equations, making it easier to solve problems and understand mathematical relationships. In this article, we will delve into the world of radical form simplified, exploring its definition, benefits, and practical applications.
Understanding Radical Form Simplified
Radical form simplified refers to the process of simplifying expressions that contain radicals, such as square roots, cube roots, and nth roots. Radicals are mathematical symbols that represent the root of a number, and they are often used to simplify complex expressions and equations. By simplifying radicals, we can make mathematical calculations more efficient and accurate.

Benefits of Radical Form Simplified
Simplifying radicals has numerous benefits in mathematics and other fields. Some of the most significant advantages include:
- Improved accuracy: Simplifying radicals reduces the likelihood of errors and inaccuracies in mathematical calculations.
- Increased efficiency: Radical form simplified makes it easier to solve complex equations and expressions, saving time and effort.
- Enhanced understanding: By simplifying radicals, we can gain a deeper understanding of mathematical relationships and concepts.
- Better problem-solving skills: Radical form simplified helps develop critical thinking and problem-solving skills, essential for mathematics and other fields.
How to Simplify Radicals
Simplifying radicals involves several steps and techniques. Here are some of the most common methods:
Step 1: Factor the Radicand
The first step in simplifying radicals is to factor the radicand, which is the number or expression inside the radical. Factoring involves breaking down the radicand into its prime factors.
Step 2: Identify Perfect Squares or Cubes
Next, identify any perfect squares or cubes within the radicand. Perfect squares and cubes can be simplified using specific rules and formulas.
Step 3: Simplify the Radical
Once you have factored the radicand and identified any perfect squares or cubes, simplify the radical using the appropriate rules and formulas.

Practical Applications of Radical Form Simplified
Radical form simplified has numerous practical applications in mathematics, science, engineering, and other fields. Some examples include:
- Algebra: Simplifying radicals is essential in algebra, particularly when solving equations and inequalities.
- Geometry: Radical form simplified is used in geometry to calculate distances, lengths, and areas of shapes.
- Trigonometry: Simplifying radicals is crucial in trigonometry, particularly when working with trigonometric identities and equations.
- Physics: Radical form simplified is used in physics to calculate velocities, accelerations, and energies.
Real-World Examples
Radical form simplified has many real-world applications, including:
- Designing roller coasters: Simplifying radicals is used to calculate the height and length of roller coaster tracks.
- Predicting population growth: Radical form simplified is used in demographics to predict population growth and decline.
- Optimizing computer networks: Simplifying radicals is used in computer science to optimize network performance and efficiency.
Common Mistakes to Avoid
When simplifying radicals, there are several common mistakes to avoid:
- Incorrect factoring: Factoring the radicand incorrectly can lead to errors and inaccuracies.
- Ignoring perfect squares or cubes: Failing to identify perfect squares or cubes can result in oversimplification or incorrect simplification.
- Applying incorrect rules: Applying incorrect rules or formulas can lead to errors and inaccuracies.

Conclusion and Final Thoughts
Radical form simplified is a powerful tool in mathematics, enabling us to simplify complex expressions and equations. By understanding the benefits, techniques, and practical applications of radical form simplified, we can improve our mathematical skills and problem-solving abilities. Remember to avoid common mistakes and practice simplifying radicals regularly to become proficient.

What's Next?
Now that you have learned about radical form simplified, it's time to practice and apply your knowledge. Try simplifying radicals in different mathematical contexts, such as algebra, geometry, and trigonometry. Experiment with different techniques and formulas to develop your problem-solving skills.
Share Your Thoughts
Do you have any questions or comments about radical form simplified? Share your thoughts and experiences in the comments section below. Let's discuss and learn from each other!
What is radical form simplified?
+Radical form simplified is the process of simplifying expressions that contain radicals, such as square roots, cube roots, and nth roots.
What are the benefits of radical form simplified?
+The benefits of radical form simplified include improved accuracy, increased efficiency, enhanced understanding, and better problem-solving skills.
How do I simplify radicals?
+To simplify radicals, factor the radicand, identify perfect squares or cubes, and apply the appropriate rules and formulas.