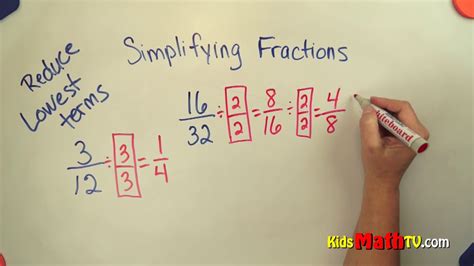Simplifying fractions to their lowest terms is an essential math skill that can help you work more efficiently with numbers. When we simplify a fraction, we reduce it to its most basic form by dividing both the numerator and the denominator by their greatest common divisor (GCD). In this article, we will explore 7 ways to simplify the fraction 78 to its lowest term.
Understanding Fractions and Simplification
Before we dive into the methods, let's briefly review what fractions are and why simplifying them is important. A fraction represents a part of a whole as a ratio of two numbers. The top number, called the numerator, tells us how many equal parts we have, while the bottom number, the denominator, tells us how many parts the whole is divided into. Simplifying fractions makes it easier to compare, add, subtract, multiply, and divide them.

Method 1: Finding the Greatest Common Divisor (GCD)
The most straightforward way to simplify a fraction is by dividing both the numerator and the denominator by their GCD. To find the GCD of 78, we first need to list all the factors of 78. The factors of 78 are 1, 2, 3, 6, 9, 13, 18, 26, 39, and 78.

Step-by-Step Process
- List all the factors of 78.
- Identify the greatest common divisor among the factors.
- Divide both the numerator and the denominator by the GCD.
Method 2: Prime Factorization
Another method to simplify fractions is by using prime factorization. This involves breaking down both the numerator and the denominator into their prime factors and then canceling out any common factors.

Step-by-Step Process
- Break down 78 into its prime factors.
- Identify any common factors between the numerator and the denominator.
- Cancel out the common factors.
Method 3: Using the Euclidean Algorithm
The Euclidean algorithm is a systematic way of finding the GCD of two numbers, which can be used to simplify fractions. This method involves a series of steps where we divide the larger number by the smaller number and take the remainder.

Step-by-Step Process
- Divide the larger number by the smaller number.
- Take the remainder.
- Repeat the process until the remainder is 0.
Method 4: Simplifying with a Common Factor
If we notice that both the numerator and the denominator have a common factor, we can simplify the fraction by dividing both numbers by that factor.

Step-by-Step Process
- Identify a common factor between the numerator and the denominator.
- Divide both numbers by the common factor.
Method 5: Using a Calculator or Online Tool
In today's digital age, we can use calculators or online tools to simplify fractions quickly and accurately. These tools can save us time and effort, especially when dealing with complex fractions.

Step-by-Step Process
- Enter the fraction into the calculator or online tool.
- Press the simplify button or enter the command.
- Read the simplified fraction from the display.
Method 6: Working with Equivalent Ratios
Sometimes, we can simplify fractions by working with equivalent ratios. This involves multiplying or dividing both the numerator and the denominator by the same number to create an equivalent fraction with smaller numbers.

Step-by-Step Process
- Multiply or divide both the numerator and the denominator by the same number.
- Simplify the resulting fraction.
Method 7: Visualizing with Diagrams
Finally, we can use diagrams to visualize the fraction and simplify it. This method can be particularly helpful for students who are visual learners.

Step-by-Step Process
- Draw a diagram to represent the fraction.
- Identify the shaded region.
- Simplify the fraction based on the diagram.
By mastering these 7 methods, you can simplify fractions with ease and become more confident in your math skills.
Invite others to share their favorite methods for simplifying fractions in the comments below!