5.93 E 5 In Standard Form Conversion Made Easy

Quick Links :

Standard form conversion is a crucial concept in mathematics, particularly in scientific notation and exponential expressions. One common operation in this realm is converting a number from standard form to a more readable format. In this article, we'll delve into the world of standard form conversion, focusing on the number 5.93 E 5.

Understanding Standard Form

Standard form, also known as scientific notation, is a method of expressing numbers in a compact and easily readable format. It's commonly used in science, engineering, and mathematics to simplify complex calculations and represent extremely large or small numbers. A number in standard form is expressed as a product of a number between 1 and 10, multiplied by a power of 10.

Why is Standard Form Important?

Standard form conversion is essential in various fields, such as physics, chemistry, and engineering, where calculations often involve large or small numbers. By converting these numbers into standard form, we can:

• Simplify complex calculations
• Improve accuracy and precision
• Enhance readability and understanding
• Facilitate calculations involving extremely large or small numbers

Converting 5.93 E 5 to Standard Form

Now, let's focus on converting the number 5.93 E 5 to standard form. The "E" in this expression represents the power of 10, indicating that the number should be multiplied by 10 raised to the power of 5.

To convert this number, we need to move the decimal point five places to the right, as indicated by the exponent 5. This results in the number 593,000.

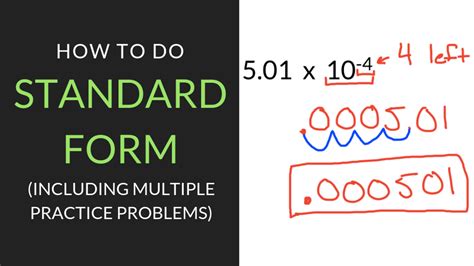
How to Convert a Number from Standard Form to a Readable Format

Converting a number from standard form to a more readable format involves a simple process:

1. Identify the exponent (the number after the "E")
2. Move the decimal point the same number of places as the exponent
3. If the exponent is positive, move the decimal point to the right
4. If the exponent is negative, move the decimal point to the left

Examples and Practical Applications

To illustrate the concept of standard form conversion, let's consider a few examples:

• Convert 3.45 E 2 to a readable format:
  • Move the decimal point two places to the right
  • Result: 345
• Convert 2.78 E -3 to a readable format:
  • Move the decimal point three places to the left
  • Result: 0.00278

Standard form conversion has numerous practical applications, such as:

• Calculating the mass of an object in kilograms or grams
• Measuring the length of an object in meters or centimeters
• Expressing the volume of a substance in liters or milliliters

Common Mistakes and Misconceptions

When working with standard form conversion, it's essential to avoid common mistakes and misconceptions:

• Incorrectly moving the decimal point
• Forgetting to consider the sign of the exponent
• Confusing the exponent with the coefficient

Conclusion and Next Steps

In conclusion, standard form conversion is a fundamental concept in mathematics and science. By mastering this skill, you can simplify complex calculations, improve accuracy, and enhance readability. To further develop your understanding, practice converting numbers from standard form to readable formats, and explore practical applications in various fields.

We invite you to share your thoughts and questions in the comments below. How do you use standard form conversion in your work or studies? What challenges have you faced, and how have you overcome them? Your input will help us create more informative and engaging content for our readers.