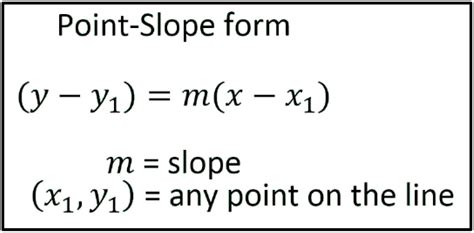Write Equations In Point Slope Form With Ease

Quick Links :

Writing equations in point-slope form is an essential skill for anyone studying algebra or geometry. In this article, we'll explore the ins and outs of point-slope form, including its definition, benefits, and step-by-step instructions on how to write equations in this form with ease.

What is Point-Slope Form?

Point-slope form is a way of writing the equation of a line using the slope-intercept form, which is typically represented as y = mx + b. However, in point-slope form, the equation is written as y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.

Benefits of Point-Slope Form

So, why use point-slope form instead of slope-intercept form? Here are a few benefits:

• Point-slope form is particularly useful when you're given a point on the line and the slope. It makes it easy to write the equation of the line.
• It's also helpful when you're working with lines that are not in the standard position (i.e., not horizontal or vertical).
• Point-slope form can be used to find the equation of a line that passes through two points.

How to Write Equations in Point-Slope Form

Now that we've covered the benefits of point-slope form, let's dive into the step-by-step process of writing equations in this form.

Step 1: Identify the Point and Slope

The first step is to identify the point (x1, y1) and the slope (m) of the line. This information can be given to you in the problem, or you may need to find it using other information.

Step 2: Plug in the Values

Once you have the point and slope, plug these values into the point-slope form equation: y - y1 = m(x - x1).

Step 3: Simplify the Equation

After plugging in the values, simplify the equation by distributing the slope (m) to the terms inside the parentheses.

Step 4: Write the Final Equation

The resulting equation is the final answer. Make sure to check your work by plugging in the point (x1, y1) to ensure that it satisfies the equation.

Example Problems

Let's work through a few example problems to illustrate the process.

Example 1:

Find the equation of the line that passes through the point (2, 3) and has a slope of 4.

• Step 1: Identify the point and slope. The point is (2, 3), and the slope is 4.
• Step 2: Plug in the values. y - 3 = 4(x - 2)
• Step 3: Simplify the equation. y - 3 = 4x - 8
• Step 4: Write the final equation. y = 4x - 5

Example 2:

Find the equation of the line that passes through the points (1, 2) and (3, 4).

• Step 1: Identify the points. The points are (1, 2) and (3, 4).
• Step 2: Find the slope. The slope is (4 - 2) / (3 - 1) = 1.
• Step 3: Plug in the values. y - 2 = 1(x - 1)
• Step 4: Simplify the equation. y - 2 = x - 1
• Step 5: Write the final equation. y = x + 1

Common Mistakes to Avoid

When working with point-slope form, there are a few common mistakes to avoid.

• Make sure to plug in the correct values for the point and slope.
• Double-check your work by plugging in the point (x1, y1) to ensure that it satisfies the equation.
• Be careful when simplifying the equation, as it's easy to make algebraic mistakes.

Conclusion: Mastering Point-Slope Form

Writing equations in point-slope form is a valuable skill that can help you solve a variety of problems in algebra and geometry. By following the step-by-step process outlined in this article, you can master point-slope form and become proficient in writing equations of lines.

We hope this article has been informative and helpful. If you have any questions or comments, please don't hesitate to reach out. Share this article with your friends and classmates who may be struggling with point-slope form.

FAQ Section: