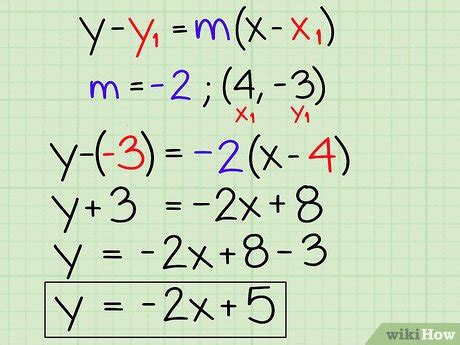Writing Equations In Slope-Intercept Form Made Easy

Quick Links :

Hide

Learning to write equations in slope-intercept form is a crucial skill for any student of algebra. It's a fundamental concept that can seem daunting at first, but with practice and patience, it can become second nature. In this article, we'll break down the basics of slope-intercept form, provide examples, and offer tips and tricks to make writing equations in this form a breeze.

What is Slope-Intercept Form?

Slope-intercept form is a way of writing a linear equation in the form y = mx + b, where:

• m is the slope of the line
• b is the y-intercept (the point where the line crosses the y-axis)

This form is useful because it allows us to easily identify the slope and y-intercept of a line, which are essential components of linear equations.

How to Write Equations in Slope-Intercept Form

Writing an equation in slope-intercept form is relatively straightforward. Here are the steps:

1. Identify the slope (m) of the line. This can be found using the formula m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
2. Identify the y-intercept (b) of the line. This can be found by substituting one of the points on the line into the equation and solving for b.
3. Write the equation in the form y = mx + b.

For example, let's say we want to write an equation for the line that passes through the points (2, 3) and (4, 5).

First, we find the slope (m) using the formula:

m = (5 - 3) / (4 - 2) m = 2 / 2 m = 1

Next, we find the y-intercept (b) by substituting one of the points into the equation:

3 = 1(2) + b 3 = 2 + b b = 1

Finally, we write the equation in slope-intercept form:

y = x + 1

Examples and Applications

Slope-intercept form is used in a wide range of applications, from physics and engineering to economics and computer science. Here are a few examples:

• In physics, the equation for the motion of an object can be written in slope-intercept form, where the slope represents the acceleration and the y-intercept represents the initial velocity.
• In economics, the equation for the supply and demand of a product can be written in slope-intercept form, where the slope represents the elasticity of the market and the y-intercept represents the equilibrium price.
• In computer science, the equation for a line can be written in slope-intercept form, where the slope represents the rate of change of the output and the y-intercept represents the initial value of the output.

Tips and Tricks for Writing Equations in Slope-Intercept Form

Here are a few tips and tricks to help you write equations in slope-intercept form:

• Make sure to identify the slope and y-intercept correctly. This is crucial for writing the equation correctly.
• Use the formula for slope to find the slope of the line.
• Use substitution to find the y-intercept of the line.
• Practice, practice, practice! The more you practice writing equations in slope-intercept form, the more comfortable you'll become with the process.

Common Mistakes to Avoid

Here are a few common mistakes to avoid when writing equations in slope-intercept form:

• Writing the equation in the wrong form. Make sure to write the equation in the form y = mx + b.
• Confusing the slope and y-intercept. Make sure to identify the slope and y-intercept correctly.
• Not using the formula for slope. Use the formula to find the slope of the line.

Conclusion

Writing equations in slope-intercept form is a fundamental skill in algebra. With practice and patience, it can become second nature. By following the steps outlined in this article and avoiding common mistakes, you'll be well on your way to writing equations in slope-intercept form with ease.