The world of algebra and linear equations can be a fascinating yet daunting realm for many students. One of the most fundamental concepts in this domain is the Slope-Intercept Form, which is a way of expressing linear equations in a concise and informative manner. In this article, we will delve into the concept of Slope-Intercept Form, explore its significance, and examine the specific example of 3x 5y 15 in Slope-Intercept Form.
Understanding Slope-Intercept Form
The Slope-Intercept Form is a way of expressing linear equations in the form y = mx + b, where:
- m represents the slope of the line
- b represents the y-intercept of the line
- x is the independent variable
- y is the dependent variable
This form is incredibly useful because it allows us to easily identify the slope and y-intercept of a line, which are crucial in understanding the behavior of the line.
Why is Slope-Intercept Form Important?
The Slope-Intercept Form is essential in algebra and mathematics because it provides a concise and informative way of expressing linear equations. This form is particularly useful in:
- Graphing lines: By knowing the slope and y-intercept, we can easily graph lines on a coordinate plane.
- Solving systems of equations: The Slope-Intercept Form makes it easier to solve systems of linear equations.
- Analyzing functions: The Slope-Intercept Form helps us understand the behavior of functions, including their rate of change and maximum/minimum values.
Converting to Slope-Intercept Form
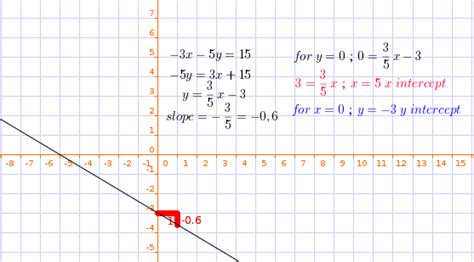
To convert a linear equation to Slope-Intercept Form, we need to isolate the variable y. Let's take the example of 3x 5y 15.

First, we need to add 5y to both sides of the equation to get:
3x 15 = 5y
Next, we divide both sides of the equation by 5 to get:
(3/5)x 3 = y
Finally, we rearrange the equation to get it in Slope-Intercept Form:
y = (3/5)x 3
Analyzing the Slope-Intercept Form
Now that we have the equation in Slope-Intercept Form, let's analyze its components.
- Slope (m): The slope of the line is 3/5, which means that for every 5 units we move to the right, the line rises by 3 units.
- Y-intercept (b): The y-intercept of the line is 3, which means that the line crosses the y-axis at the point (0, 3).
Practical Applications of Slope-Intercept Form
The Slope-Intercept Form has numerous practical applications in various fields, including:
- Physics: The Slope-Intercept Form is used to model the motion of objects, including their velocity and acceleration.
- Economics: The Slope-Intercept Form is used to model the behavior of economic systems, including supply and demand curves.
- Computer Science: The Slope-Intercept Form is used in algorithms for graphing and solving systems of linear equations.
Conclusion and Next Steps
In conclusion, the Slope-Intercept Form is a powerful tool for expressing linear equations in a concise and informative manner. By understanding the Slope-Intercept Form, we can gain insights into the behavior of lines and functions, which has numerous practical applications in various fields.
If you have any questions or would like to explore more topics in algebra and mathematics, please leave a comment below. We'd love to hear from you!
What is the Slope-Intercept Form?
+The Slope-Intercept Form is a way of expressing linear equations in the form y = mx + b, where m represents the slope and b represents the y-intercept.
Why is the Slope-Intercept Form important?
+The Slope-Intercept Form is essential in algebra and mathematics because it provides a concise and informative way of expressing linear equations, making it easier to graph lines, solve systems of equations, and analyze functions.
How do I convert a linear equation to Slope-Intercept Form?
+To convert a linear equation to Slope-Intercept Form, isolate the variable y by adding and subtracting the same value to both sides of the equation, and then rearrange the equation to get it in the form y = mx + b.