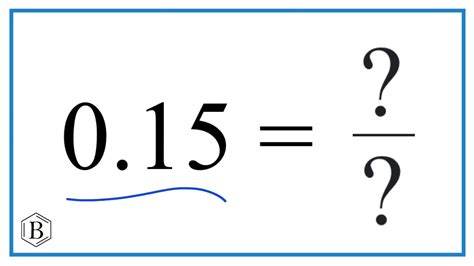The number 15 can be expressed in fraction form in various ways, depending on the desired denominator. Here are a few examples:
- 15/1: This is the simplest fraction form of 15, with a denominator of 1.
- 30/2: This fraction is equivalent to 15, with a numerator of 30 and a denominator of 2.
- 45/3: This fraction is also equivalent to 15, with a numerator of 45 and a denominator of 3.
In general, any fraction with a numerator that is a multiple of 15 and a denominator that is a factor of 15 will be equivalent to 15. Some other examples include:
- 60/4
- 75/5
- 90/6
- 120/8
It's worth noting that 15 can also be expressed as a mixed fraction, which is a combination of a whole number and a proper fraction. For example:
- 15 = 14 1/1
- 15 = 13 2/2
- 15 = 12 3/3
These mixed fractions can be useful in certain mathematical contexts, but they are not as commonly used as the simple fraction forms listed above.
What is a Fraction?
A fraction is a way to express a part of a whole as a numerical value. It consists of a numerator (the top number) and a denominator (the bottom number), separated by a horizontal line. The numerator represents the number of equal parts, and the denominator represents the total number of parts.
For example, the fraction 3/4 represents three equal parts out of a total of four parts. Fractions can be used to represent a wide range of mathematical concepts, including proportions, ratios, and decimals.
Why Use Fractions?
Fractions are an essential part of mathematics, and they have many real-world applications. Here are a few reasons why fractions are useful:
- Measurement: Fractions are used to measure quantities that are not whole numbers. For example, a recipe might call for 3/4 cup of flour.
- Ratios: Fractions are used to express ratios, or comparisons between two quantities. For example, a car might travel 3/4 of a mile in 1 minute.
- Decimals: Fractions can be converted to decimals, which are used in many mathematical and scientific applications.
- Percentages: Fractions can be converted to percentages, which are used to express proportions and rates of change.
How to Simplify Fractions
Simplifying fractions is an important mathematical skill that can help you to work with fractions more easily. To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and denominator, and then divide both numbers by the GCD.
For example, the fraction 6/8 can be simplified by dividing both numbers by 2, resulting in 3/4. This is because 2 is the greatest common divisor of 6 and 8.
Here are the steps to simplify a fraction:
- Find the greatest common divisor (GCD) of the numerator and denominator.
- Divide the numerator and denominator by the GCD.
- The resulting fraction is the simplified form.
Common Fraction Operations
Fractions can be added, subtracted, multiplied, and divided, just like whole numbers. However, the operations are slightly different. Here are the basic rules for fraction operations:
- Addition: To add fractions, you need to have the same denominator. If the denominators are different, you need to find the least common multiple (LCM) and convert both fractions to have the LCM as the denominator.
- Subtraction: To subtract fractions, you need to have the same denominator. If the denominators are different, you need to find the LCM and convert both fractions to have the LCM as the denominator.
- Multiplication: To multiply fractions, you need to multiply the numerators and multiply the denominators.
- Division: To divide fractions, you need to invert the second fraction (i.e. flip the numerator and denominator) and then multiply.
For example, to add the fractions 1/4 and 1/6, you need to find the LCM of 4 and 6, which is 12. You can then convert both fractions to have a denominator of 12:
- 1/4 = 3/12
- 1/6 = 2/12
The sum of the fractions is 3/12 + 2/12 = 5/12.

Conclusion
Fractions are an essential part of mathematics, and they have many real-world applications. Understanding fractions can help you to work with proportions, ratios, and decimals, and to solve problems in a wide range of mathematical and scientific contexts.
By mastering the basics of fractions, including simplifying, adding, subtracting, multiplying, and dividing, you can develop a strong foundation in mathematics and improve your problem-solving skills.
We hope this article has helped you to understand fractions better. Do you have any questions about fractions? Leave a comment below and let us know!
FAQs
What is a fraction?
+A fraction is a way to express a part of a whole as a numerical value. It consists of a numerator (the top number) and a denominator (the bottom number), separated by a horizontal line.
Why are fractions important?
+Fractions are important because they are used to measure quantities that are not whole numbers, express ratios and proportions, and convert to decimals and percentages.
How do I simplify a fraction?
+To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and denominator, and then divide both numbers by the GCD.