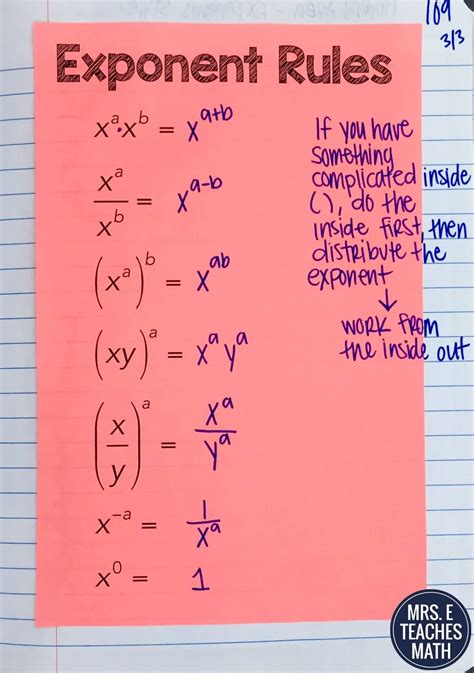Master 1 In Exponential Form In 5 Easy Steps

Quick Links :

The concept of exponential form can seem daunting at first, but with a clear understanding of the basics and a step-by-step approach, you can master it in no time. Exponential form is a fundamental concept in mathematics, and being proficient in it can open doors to understanding more complex mathematical concepts.

In this article, we will break down the concept of exponential form into five easy-to-follow steps. By the end of this article, you will be able to convert numbers into exponential form, simplify exponential expressions, and understand the applications of exponential form in real-life scenarios.

Step 1: Understanding the Basics of Exponential Form

Exponential form is a way of expressing numbers in terms of their base and exponent. It is a shorthand method of representing repeated multiplication. For example, the number 2^3 can be expressed as 2 × 2 × 2. In this case, 2 is the base, and 3 is the exponent.

To understand exponential form, you need to grasp the concept of powers. A power is a number raised to a certain exponent. For instance, 2^3 is a power, where 2 is the base, and 3 is the exponent.

Key Concepts to Remember:

• Base: The number being raised to a power.
• Exponent: The power to which the base is raised.
• Power: A number raised to a certain exponent.

Step 2: Converting Numbers to Exponential Form

Now that you understand the basics of exponential form, it's time to learn how to convert numbers into exponential form. The process is straightforward:

1. Identify the base and exponent.
2. Write the base as a power with the exponent as the power to which it is raised.

For example, let's convert the number 8 into exponential form:

• Base: 2
• Exponent: 3
• Exponential form: 2^3

Here are a few more examples:

• 16 = 2^4
• 32 = 2^5
• 64 = 2^6

Tips and Tricks:

• Start with simple numbers and gradually move on to more complex ones.
• Practice converting different numbers to exponential form to get a feel for the process.

Step 3: Simplifying Exponential Expressions

Simplifying exponential expressions involves applying the rules of exponents to simplify complex expressions. Here are the basic rules:

• Product of powers: a^m × a^n = a^(m+n)
• Power of a power: (a^m)^n = a^(m×n)
• Quotient of powers: a^m ÷ a^n = a^(m-n)

For example, let's simplify the expression:

• 2^3 × 2^4 = 2^(3+4) = 2^7

Here are a few more examples:

• (2^3)^2 = 2^(3×2) = 2^6
• 2^5 ÷ 2^2 = 2^(5-2) = 2^3

Key Concepts to Remember:

• Product of powers: Combine the exponents by adding them.
• Power of a power: Multiply the exponents.
• Quotient of powers: Subtract the exponents.

Step 4: Applying Exponential Form in Real-Life Scenarios

Exponential form has numerous applications in real-life scenarios, including:

• Finance: Compound interest, exponential growth of investments.
• Science: Population growth, exponential decay of radioactive substances.
• Computer Science: Algorithm complexity, exponential time complexity.

For example, let's consider a scenario where you invest $1000 at an annual interest rate of 5%. After one year, your investment will grow to:

• $1000 × (1 + 0.05) = $1050

Using exponential form, we can represent this growth as:

• $1000 × (1.05)^1 = $1050

Here are a few more examples:

• Population growth: A city's population grows at an annual rate of 2%. If the current population is 100,000, what will it be after 5 years? (Answer: 100,000 × (1.02)^5 = 110,408)
• Exponential decay: A radioactive substance decays at a rate of 10% per hour. If the initial amount is 100g, what will it be after 2 hours? (Answer: 100g × (0.9)^2 = 81g)

Tips and Tricks:

• Use real-life scenarios to practice applying exponential form.
• Start with simple examples and gradually move on to more complex ones.

Step 5: Practicing Exponential Form with Sample Questions

Now that you have a solid understanding of exponential form, it's time to practice with sample questions. Here are a few examples:

• Simplify the expression: 2^3 × 2^2 =?
• Convert the number 256 to exponential form.
• A population grows at an annual rate of 3%. If the current population is 500,000, what will it be after 2 years?

Answer Key:

• 2^3 × 2^2 = 2^5
• 256 = 2^8
• 500,000 × (1.03)^2 = 530,450

By practicing with sample questions, you can reinforce your understanding of exponential form and become more confident in your ability to apply it in real-life scenarios.

In conclusion, mastering exponential form in 5 easy steps requires a clear understanding of the basics, practice, and application in real-life scenarios. By following these steps and practicing with sample questions, you can become proficient in exponential form and unlock the doors to more complex mathematical concepts.