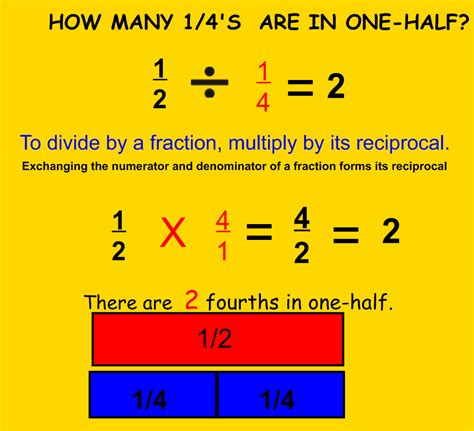
The concept of fractions is a fundamental part of mathematics, allowing us to represent and work with parts of a whole. When dealing with fractions, understanding how to divide them is crucial for solving various mathematical problems. In this article, we'll explore how to divide one quarter by 5 in fraction form, explaining the steps and concepts involved in this mathematical operation.
Understanding Fractions

Fractions are a way to express a part of a whole as a ratio of two numbers. The top number, known as the numerator, tells us how many equal parts we have, while the bottom number, or denominator, tells us how many parts the whole is divided into. For example, in the fraction 1/4, the numerator is 1, and the denominator is 4, meaning we have one part out of a total of four equal parts.
The Concept of Division in Fractions
Division in fractions involves finding how many times one fraction fits into another. When dividing fractions, we need to invert the second fraction (i.e., flip the numerator and denominator) and then multiply. This rule applies to all division operations involving fractions.
Dividing One Quarter by 5

To divide one quarter (1/4) by 5, we first need to convert the whole number 5 into a fraction. Since 5 can be represented as 5/1, our division problem looks like this:
(1/4) ÷ (5/1)
Following the rule for dividing fractions, we invert the second fraction (5/1 becomes 1/5) and then multiply:
(1/4) × (1/5)
Multiplying Fractions
When multiplying fractions, we simply multiply the numerators together to get the new numerator and multiply the denominators together to get the new denominator. So, for our problem:
(1 × 1) / (4 × 5) = 1/20
Therefore, one quarter divided by 5 in fraction form is 1/20.
Practical Applications and Examples

Understanding how to divide fractions is crucial in various real-world applications, from cooking and measuring ingredients to scientific calculations and financial analyses. Here are a few examples:
- Cooking: When a recipe requires 1/4 cup of an ingredient, and you want to make only a fifth of the recipe, you would need 1/20 of a cup of that ingredient.
- Science: In scientific research, dividing fractions might be necessary for calculating concentrations of solutions or measuring the areas of land.
- Finance: Dividing fractions can be useful in financial calculations, such as determining investment returns or dividing assets.
Conclusion and Further Learning
Dividing fractions is a fundamental mathematical operation that, once mastered, opens up a wide range of problem-solving possibilities. By understanding how to divide one quarter by 5 in fraction form, we've demonstrated the basic steps and rules involved in this process. To further your learning, practice dividing different fractions and explore more complex operations involving fractions, such as adding and subtracting mixed numbers.
What is the rule for dividing fractions?
+To divide fractions, you invert the second fraction (flip the numerator and denominator) and then multiply.
How do you multiply fractions?
+When multiplying fractions, you multiply the numerators together to get the new numerator and multiply the denominators together to get the new denominator.
Why is dividing fractions useful in real-world applications?
+Dividing fractions is useful in various applications, including cooking, scientific calculations, and financial analyses, allowing for precise measurements and calculations.