0.46 As A Fraction In Simplest Form

Quick Links :

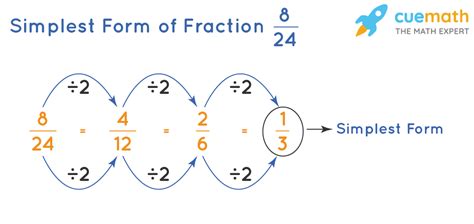
The decimal number 0.46 can be converted to a fraction in simplest form by following these steps:

First, we need to determine the place value of the decimal number. Since 0.46 has two digits after the decimal point, we can multiply it by 100 to eliminate the decimal.

0.46 × 100 = 46

Now, we can write 0.46 as a fraction:

0.46 = 46/100

To simplify the fraction, we need to find the greatest common divisor (GCD) of the numerator (46) and the denominator (100).

The factors of 46 are: 1, 2, 23, 46 The factors of 100 are: 1, 2, 4, 5, 10, 20, 25, 50, 100

The GCD of 46 and 100 is 2.

Now, we can divide both the numerator and the denominator by the GCD to simplify the fraction:

46 ÷ 2 = 23 100 ÷ 2 = 50

So, the simplified fraction is:

0.46 = 23/50

Therefore, 0.46 as a fraction in simplest form is 23/50.

Understanding Fractions

Fractions are a way to represent part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator tells us how many equal parts we have, and the denominator tells us how many parts the whole is divided into.

For example, the fraction 3/4 means we have 3 equal parts out of a total of 4 parts.

Fractions can be classified into different types, including:

• Proper Fractions

Proper fractions are fractions where the numerator is less than the denominator. For example, 3/4 is a proper fraction.

• Improper Fractions

Improper fractions are fractions where the numerator is greater than or equal to the denominator. For example, 4/3 is an improper fraction.

• Mixed Numbers

Mixed numbers are a combination of a whole number and a proper fraction. For example, 2 3/4 is a mixed number.

• Equivalent Fractions

Equivalent fractions are fractions that have the same value but different forms. For example, 1/2 and 2/4 are equivalent fractions.

Adding and Subtracting Fractions

To add or subtract fractions, we need to follow these steps:

• Step 1: Check if the denominators are the same

If the denominators are the same, we can add or subtract the numerators directly.

• Step 2: Find the least common multiple (LCM) of the denominators

If the denominators are different, we need to find the LCM of the denominators. The LCM is the smallest number that both denominators can divide into evenly.

• Step 3: Convert the fractions to have the same denominator

Once we have the LCM, we can convert both fractions to have the same denominator by multiplying the numerator and the denominator by the necessary multiple.

• Step 4: Add or subtract the fractions

Now that the fractions have the same denominator, we can add or subtract the numerators directly.

Multiplying and Dividing Fractions

To multiply fractions, we need to follow these steps:

• Step 1: Multiply the numerators

Multiply the numerators (the top numbers) together.

• Step 2: Multiply the denominators

Multiply the denominators (the bottom numbers) together.

• Step 3: Simplify the fraction

Simplify the resulting fraction by dividing both the numerator and the denominator by the greatest common divisor (GCD).

To divide fractions, we need to follow these steps:

• Step 1: Invert the second fraction

Invert the second fraction by flipping the numerator and the denominator.

• Step 2: Multiply the fractions

Multiply the fractions as usual.

Real-World Applications of Fractions

Fractions have many real-world applications, including:

• Cooking and Recipes

Fractions are often used in cooking and recipes to measure ingredients.

• Science and Engineering

Fractions are used in science and engineering to represent proportions and ratios.

• Finance and Business

Fractions are used in finance and business to calculate interest rates, investment returns, and other financial metrics.

In conclusion, fractions are an essential part of mathematics and have many real-world applications. Understanding fractions can help us solve problems and make informed decisions in various fields.

We hope this article has helped you understand fractions better. If you have any questions or need further clarification, please don't hesitate to ask.