5 Ways To Write Quadratic Functions In Standard Form

Quick Links :

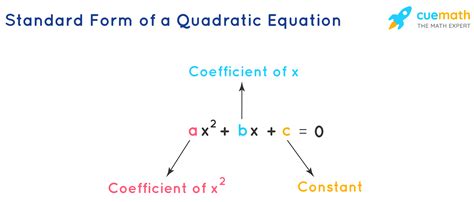
Quadratic functions are a fundamental concept in algebra, and writing them in standard form is an essential skill for any math student. Standard form of a quadratic function is ax^2 + bx + c, where a, b, and c are constants, and a cannot be zero. In this article, we will explore five ways to write quadratic functions in standard form.

Method 1: Factoring

Factoring is a popular method for writing quadratic functions in standard form. This method involves expressing the quadratic function as a product of two binomials. The factored form of a quadratic function is (x - r)(x - s), where r and s are the roots of the function.

To write a quadratic function in standard form using factoring, follow these steps:

• Identify the roots of the function, r and s.
• Write the factored form of the function, (x - r)(x - s).
• Multiply the two binomials to obtain the standard form, ax^2 + bx + c.

For example, consider the quadratic function (x - 2)(x + 3). To write this function in standard form, we multiply the two binomials:

(x - 2)(x + 3) = x^2 + 3x - 2x - 6 = x^2 + x - 6

Therefore, the standard form of the quadratic function is x^2 + x - 6.

Example 1: Factoring a Quadratic Function

Write the quadratic function (x + 1)(x - 4) in standard form.

Solution: Multiply the two binomials:

(x + 1)(x - 4) = x^2 - 4x + x - 4 = x^2 - 3x - 4

Therefore, the standard form of the quadratic function is x^2 - 3x - 4.

Method 2: Completing the Square

Completing the square is another method for writing quadratic functions in standard form. This method involves manipulating the quadratic function to create a perfect square trinomial.

To write a quadratic function in standard form using completing the square, follow these steps:

• Write the quadratic function in the form ax^2 + bx + c.
• Move the constant term to the right-hand side of the equation.
• Add and subtract (b/2)^2 to the left-hand side of the equation.
• Factor the perfect square trinomial.

For example, consider the quadratic function x^2 + 6x + 8. To write this function in standard form using completing the square, follow these steps:

x^2 + 6x + 8 = (x^2 + 6x + 9) - 1 = (x + 3)^2 - 1

Therefore, the standard form of the quadratic function is (x + 3)^2 - 1.

Example 2: Completing the Square

Write the quadratic function x^2 + 4x + 3 in standard form using completing the square.

Solution: Move the constant term to the right-hand side of the equation:

x^2 + 4x = -3

Add and subtract (b/2)^2 to the left-hand side of the equation:

x^2 + 4x + 4 = -3 + 4 = (x + 2)^2 - 1

Therefore, the standard form of the quadratic function is (x + 2)^2 - 1.

Method 3: Using the Quadratic Formula

The quadratic formula is a powerful tool for writing quadratic functions in standard form. The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a.

To write a quadratic function in standard form using the quadratic formula, follow these steps:

• Write the quadratic function in the form ax^2 + bx + c.
• Identify the values of a, b, and c.
• Plug these values into the quadratic formula.
• Simplify the expression to obtain the standard form.

For example, consider the quadratic function x^2 + 5x + 6. To write this function in standard form using the quadratic formula, follow these steps:

x = (-5 ± √(5^2 - 4(1)(6))) / 2(1) = (-5 ± √(25 - 24)) / 2 = (-5 ± √1) / 2 = (-5 ± 1) / 2

Therefore, the standard form of the quadratic function is (x + 2)(x + 3).

Example 3: Using the Quadratic Formula

Write the quadratic function x^2 + 3x + 2 in standard form using the quadratic formula.

Solution: Identify the values of a, b, and c:

a = 1, b = 3, c = 2

Plug these values into the quadratic formula:

x = (-3 ± √(3^2 - 4(1)(2))) / 2(1) = (-3 ± √(9 - 8)) / 2 = (-3 ± √1) / 2 = (-3 ± 1) / 2

Therefore, the standard form of the quadratic function is (x + 1)(x + 2).

Method 4: Using a Graphing Calculator

A graphing calculator is a powerful tool for writing quadratic functions in standard form. To write a quadratic function in standard form using a graphing calculator, follow these steps:

• Enter the quadratic function into the calculator.
• Graph the function.
• Identify the vertex of the parabola.
• Write the equation of the parabola in vertex form, y = a(x - h)^2 + k.
• Convert the vertex form to standard form, ax^2 + bx + c.

For example, consider the quadratic function x^2 + 2x + 1. To write this function in standard form using a graphing calculator, follow these steps:

Enter the quadratic function into the calculator:

x^2 + 2x + 1

Graph the function:

The graph of the parabola is a vertical parabola that opens upward.

Identify the vertex of the parabola:

The vertex of the parabola is (-1, 0).

Write the equation of the parabola in vertex form:

y = (x + 1)^2

Convert the vertex form to standard form:

y = x^2 + 2x + 1

Therefore, the standard form of the quadratic function is x^2 + 2x + 1.

Example 4: Using a Graphing Calculator

Write the quadratic function x^2 + 4x + 4 in standard form using a graphing calculator.

Solution: Enter the quadratic function into the calculator:

x^2 + 4x + 4

Graph the function:

The graph of the parabola is a vertical parabola that opens upward.

Identify the vertex of the parabola:

The vertex of the parabola is (-2, 0).

Write the equation of the parabola in vertex form:

y = (x + 2)^2

Convert the vertex form to standard form:

y = x^2 + 4x + 4

Therefore, the standard form of the quadratic function is x^2 + 4x + 4.

Method 5: Using Algebraic Manipulation

Algebraic manipulation is a powerful tool for writing quadratic functions in standard form. This method involves manipulating the quadratic function to create a perfect square trinomial.

To write a quadratic function in standard form using algebraic manipulation, follow these steps:

• Write the quadratic function in the form ax^2 + bx + c.
• Factor out the coefficient of x^2, a.
• Complete the square by adding and subtracting (b/2)^2.
• Factor the perfect square trinomial.

For example, consider the quadratic function x^2 + 6x + 8. To write this function in standard form using algebraic manipulation, follow these steps:

Factor out the coefficient of x^2, 1:

x^2 + 6x + 8 = (x^2 + 6x + 9) - 1

Complete the square by adding and subtracting (b/2)^2:

x^2 + 6x + 9 = (x + 3)^2

Factor the perfect square trinomial:

(x + 3)^2 - 1

Therefore, the standard form of the quadratic function is (x + 3)^2 - 1.

Example 5: Using Algebraic Manipulation

Write the quadratic function x^2 + 4x + 3 in standard form using algebraic manipulation.

Solution: Factor out the coefficient of x^2, 1:

x^2 + 4x + 3 = (x^2 + 4x + 4) - 1

Complete the square by adding and subtracting (b/2)^2:

x^2 + 4x + 4 = (x + 2)^2

Factor the perfect square trinomial:

(x + 2)^2 - 1

Therefore, the standard form of the quadratic function is (x + 2)^2 - 1.

In conclusion, writing quadratic functions in standard form is an essential skill for any math student. In this article, we explored five methods for writing quadratic functions in standard form: factoring, completing the square, using the quadratic formula, using a graphing calculator, and using algebraic manipulation. Each method has its own strengths and weaknesses, and the choice of method will depend on the specific problem and the student's personal preference.

We hope this article has been informative and helpful in your understanding of quadratic functions. Do you have any questions or comments about writing quadratic functions in standard form? Share your thoughts in the comments section below!