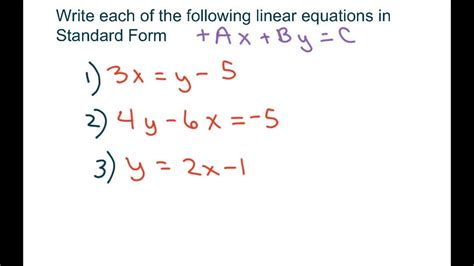5 Ways To Write Equations In Standard Form

Quick Links :

Equations are a fundamental part of mathematics, and being able to write them in standard form is a crucial skill for any math student. In this article, we'll explore five different methods for writing equations in standard form, along with examples and explanations to help you understand each approach.

Writing equations in standard form is essential because it allows us to easily compare and solve equations. Standard form also helps us to identify the key components of an equation, such as the coefficients and constants.

What is Standard Form?

Before we dive into the different methods, let's define what standard form means in the context of equations. An equation is said to be in standard form when it is written in the following format:

ax + by = c

where a, b, and c are constants, and x and y are variables. The coefficient of the x-term (a) is typically positive, and the equation is usually written with the x-term first.

Method 1: Using the General Form

One way to write an equation in standard form is to start with the general form of an equation, which is:

ax + by + c = 0

To convert this to standard form, we need to isolate the constant term (c) on one side of the equation. We can do this by adding or subtracting the same value to both sides of the equation.

For example, let's say we have the equation:

2x + 3y + 4 = 0

To write this in standard form, we can subtract 4 from both sides, giving us:

2x + 3y = -4

This is now in standard form, with the constant term isolated on the right-hand side.

Step-by-Step Example:

1. Write the equation in general form: ax + by + c = 0
2. Identify the constant term (c) and isolate it on one side of the equation.
3. Add or subtract the same value to both sides of the equation to isolate the constant term.

Method 2: Using the Slope-Intercept Form

Another way to write an equation in standard form is to start with the slope-intercept form of an equation, which is:

y = mx + b

where m is the slope and b is the y-intercept.

To convert this to standard form, we need to rewrite the equation as a linear equation in two variables.

For example, let's say we have the equation:

y = 2x + 3

To write this in standard form, we can rewrite it as:

2x - y + 3 = 0

However, this is not in standard form yet, as the coefficient of the x-term is not positive. To fix this, we can multiply both sides of the equation by -1, giving us:

-2x + y - 3 = 0

Finally, we can add 3 to both sides to isolate the constant term, giving us:

-2x + y = 3

This is now in standard form, with the coefficient of the x-term positive and the constant term isolated on the right-hand side.

Step-by-Step Example:

1. Write the equation in slope-intercept form: y = mx + b
2. Rewrite the equation as a linear equation in two variables.
3. Multiply both sides of the equation by -1 if necessary to make the coefficient of the x-term positive.
4. Add or subtract the same value to both sides of the equation to isolate the constant term.

Method 3: Using the Point-Slope Form

A third way to write an equation in standard form is to start with the point-slope form of an equation, which is:

y - y1 = m(x - x1)

where (x1, y1) is a point on the line and m is the slope.

To convert this to standard form, we need to rewrite the equation as a linear equation in two variables.

For example, let's say we have the equation:

y - 2 = 3(x - 1)

To write this in standard form, we can rewrite it as:

y - 2 = 3x - 3

Next, we can add 2 to both sides of the equation to isolate the constant term, giving us:

y = 3x - 1

However, this is not in standard form yet, as the coefficient of the x-term is not positive and the equation is not in the correct format. To fix this, we can multiply both sides of the equation by -1, giving us:

-3x + y + 1 = 0

Finally, we can subtract 1 from both sides to isolate the constant term, giving us:

-3x + y = -1

This is now in standard form, with the coefficient of the x-term positive and the constant term isolated on the right-hand side.

Step-by-Step Example:

1. Write the equation in point-slope form: y - y1 = m(x - x1)
2. Rewrite the equation as a linear equation in two variables.
3. Add or subtract the same value to both sides of the equation to isolate the constant term.
4. Multiply both sides of the equation by -1 if necessary to make the coefficient of the x-term positive.

Method 4: Using the Graphing Method

A fourth way to write an equation in standard form is to use the graphing method. This involves graphing the equation on a coordinate plane and then using the graph to find the equation of the line in standard form.

For example, let's say we have the equation:

x + 2y = 4

To graph this equation, we can plot two points on the coordinate plane and then draw a line through them.

Once we have graphed the equation, we can use the graph to find the equation of the line in standard form. In this case, the equation is already in standard form, but if it were not, we could use the graph to find the slope and y-intercept and then write the equation in standard form.

Step-by-Step Example:

1. Graph the equation on a coordinate plane.
2. Use the graph to find the slope and y-intercept of the line.
3. Write the equation of the line in slope-intercept form: y = mx + b
4. Rewrite the equation in standard form: ax + by = c

Method 5: Using the Standard Form Formula

A fifth and final way to write an equation in standard form is to use the standard form formula. This formula is:

ax + by = c

where a, b, and c are constants, and x and y are variables.

To use this formula, we simply need to plug in the values of a, b, and c to get the equation in standard form.

For example, let's say we have the equation:

2x - 3y = 5

To write this in standard form, we can simply plug the values of a, b, and c into the formula, giving us:

-2x + 3y = -5

However, this is not in standard form yet, as the coefficient of the x-term is not positive. To fix this, we can multiply both sides of the equation by -1, giving us:

2x - 3y = -5

This is now in standard form, with the coefficient of the x-term positive and the constant term isolated on the right-hand side.

Step-by-Step Example:

1. Plug the values of a, b, and c into the standard form formula: ax + by = c
2. Simplify the equation by combining like terms.
3. Multiply both sides of the equation by -1 if necessary to make the coefficient of the x-term positive.

In conclusion, there are many different ways to write an equation in standard form. By understanding the different methods and formulas, you can become proficient in writing equations in standard form and solve problems with ease.

We hope this article has been informative and helpful. Do you have any questions or topics you'd like to discuss? Share your thoughts in the comments below!