Radical expressions are a fundamental part of mathematics, and simplifying them is a crucial skill for anyone who wants to excel in math and science. Simplifying radical expressions can seem daunting at first, but with the right strategies and techniques, it can become a straightforward process. In this article, we will explore five ways to simplify radical expressions and provide examples and explanations to help you master this skill.
Understanding Radical Expressions

Before we dive into the ways to simplify radical expressions, it's essential to understand what radical expressions are and how they work. A radical expression is an expression that contains a square root, cube root, or other root symbol. The root symbol indicates that the expression inside the radical sign is being raised to a fractional exponent. For example, √x means x raised to the power of 1/2.
What Makes Radical Expressions Complicated?
Radical expressions can become complicated when they involve multiple roots, fractions, or variables. In such cases, simplifying the expression requires a step-by-step approach to ensure that the result is accurate and reliable. Complicated radical expressions can arise in various mathematical contexts, including algebra, geometry, and calculus.
Method 1: Simplifying Radical Expressions Using the Rules of Exponents

One way to simplify radical expressions is to use the rules of exponents. The rules of exponents state that when you multiply two numbers with the same base, you add their exponents. Similarly, when you divide two numbers with the same base, you subtract their exponents. You can apply these rules to simplify radical expressions by rewriting the expression using fractional exponents.
For example, consider the expression √(x^3). Using the rule of exponents, you can rewrite this expression as x^(3/2). This simplified expression is easier to work with and understand.
Example 1: Simplifying a Radical Expression Using Exponents
Simplify the expression: √(x^5)
Solution:
x^5 = x^(5/1) √(x^5) = x^(5/2)
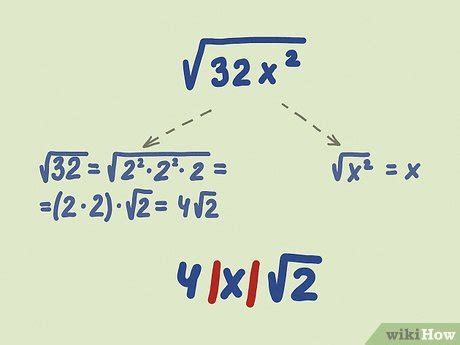
Method 2: Simplifying Radical Expressions by Factoring Out Perfect Squares

Another way to simplify radical expressions is to factor out perfect squares. A perfect square is a number that can be expressed as the square of an integer. For example, 16 is a perfect square because it can be expressed as 4^2.
When simplifying a radical expression, you can factor out perfect squares to simplify the expression. For example, consider the expression √(16x). You can factor out the perfect square 16 and rewrite the expression as 4√x.
Example 2: Simplifying a Radical Expression by Factoring Out Perfect Squares
Simplify the expression: √(48x^2)
Solution:
48 = 16 × 3 √(48x^2) = √(16 × 3 × x^2) = 4√(3x^2)
Method 3: Simplifying Radical Expressions Using Conjugate Pairs

Conjugate pairs are another useful tool for simplifying radical expressions. A conjugate pair is a pair of numbers that have the same sign and the same absolute value but opposite signs. For example, 3 + √2 and 3 - √2 are conjugate pairs.
When simplifying a radical expression, you can use conjugate pairs to eliminate the radical sign. For example, consider the expression √(3 + √2) × √(3 - √2). You can multiply these two expressions together to eliminate the radical sign.
Example 3: Simplifying a Radical Expression Using Conjugate Pairs
Simplify the expression: √(3 + √2) × √(3 - √2)
Solution:
√(3 + √2) × √(3 - √2) = √((3 + √2)(3 - √2)) = √(9 - 2) = √7
Method 4: Simplifying Radical Expressions by Rationalizing the Denominator

When simplifying radical expressions, you may encounter expressions with radicals in the denominator. To simplify such expressions, you can rationalize the denominator by multiplying the numerator and denominator by the conjugate of the denominator.
For example, consider the expression 1 / √(2 + √3). You can rationalize the denominator by multiplying the numerator and denominator by the conjugate of the denominator.
Example 4: Simplifying a Radical Expression by Rationalizing the Denominator
Simplify the expression: 1 / √(2 + √3)
Solution:
1 / √(2 + √3) = 1 / √(2 + √3) × (√(2 - √3) / √(2 - √3)) = √(2 - √3) / √((2 + √3)(2 - √3)) = √(2 - √3) / √(4 - 3) = √(2 - √3) / √1 = √(2 - √3)
Method 5: Simplifying Radical Expressions Using Algebraic Manipulations

Finally, you can simplify radical expressions using algebraic manipulations such as expanding and factoring. For example, consider the expression √(x^2 + 2x + 1). You can expand and factor the expression to simplify the radical.
Example 5: Simplifying a Radical Expression Using Algebraic Manipulations
Simplify the expression: √(x^2 + 2x + 1)
Solution:
x^2 + 2x + 1 = (x + 1)^2 √(x^2 + 2x + 1) = √((x + 1)^2) = x + 1
Conclusion: Mastering the Art of Simplifying Radical Expressions
Simplifying radical expressions is an essential skill in mathematics, and mastering this skill can help you solve complex problems with ease. By using the five methods outlined in this article, you can simplify radical expressions and take your math skills to the next level. Remember to practice regularly and use online resources to improve your understanding of radical expressions.
Call to Action: Share Your Thoughts and Questions
Do you have any questions or thoughts about simplifying radical expressions? Share them with us in the comments section below. Your feedback and questions will help us create more informative and engaging content for you.
What is a radical expression?
+A radical expression is an expression that contains a square root, cube root, or other root symbol.
Why do we need to simplify radical expressions?
+We need to simplify radical expressions to make them easier to work with and understand.
What are the five methods for simplifying radical expressions?
+The five methods for simplifying radical expressions are: using the rules of exponents, factoring out perfect squares, using conjugate pairs, rationalizing the denominator, and using algebraic manipulations.