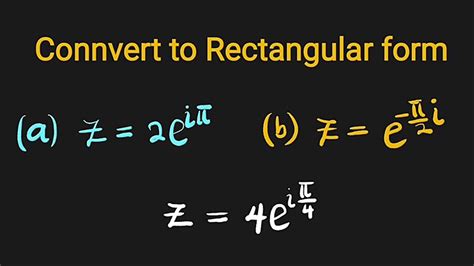Convert Complex Numbers To Rectangular And Exponential Form

Quick Links :

Complex numbers are a fundamental concept in mathematics and engineering, used to represent quantities with both magnitude and direction. They are a crucial tool for solving equations, analyzing circuits, and modeling real-world phenomena. However, complex numbers can be tricky to work with, especially when they are expressed in their standard form. To simplify calculations and gain a deeper understanding of complex numbers, it's often necessary to convert them to rectangular and exponential forms.

Understanding Complex Numbers

A complex number is a number that can be expressed in the form a + bj, where a and b are real numbers, and j is the imaginary unit, which satisfies j^2 = -1. The real part of the complex number is a, and the imaginary part is b. Complex numbers can be represented graphically on the complex plane, with the real part on the x-axis and the imaginary part on the y-axis.

Rectangular Form

The rectangular form of a complex number is given by z = a + bj, where a and b are the real and imaginary parts, respectively. This form is also known as the Cartesian form. The rectangular form is useful for adding and subtracting complex numbers, as well as for finding the magnitude and direction of a complex number.

To convert a complex number to rectangular form, we can use the following steps:

• Identify the real and imaginary parts of the complex number.
• Write the complex number in the form a + bj.

For example, suppose we want to convert the complex number 3 + 4j to rectangular form. The real part is 3, and the imaginary part is 4, so we can write the complex number as z = 3 + 4j.

Exponential Form

The exponential form of a complex number is given by z = re^(jθ), where r is the magnitude of the complex number, and θ is the angle in standard position. This form is also known as the polar form. The exponential form is useful for multiplying and dividing complex numbers, as well as for finding the roots of complex numbers.

To convert a complex number to exponential form, we can use the following steps:

• Find the magnitude of the complex number using the formula r = √(a^2 + b^2).
• Find the angle in standard position using the formula θ = arctan(b/a).
• Write the complex number in the form re^(jθ).

For example, suppose we want to convert the complex number 3 + 4j to exponential form. The magnitude is r = √(3^2 + 4^2) = 5, and the angle is θ = arctan(4/3) = 53.13°. So, we can write the complex number as z = 5e^(j53.13°).

Converting Between Rectangular and Exponential Forms

Converting between rectangular and exponential forms is a crucial skill in working with complex numbers. To convert from rectangular form to exponential form, we can use the following steps:

• Find the magnitude of the complex number using the formula r = √(a^2 + b^2).
• Find the angle in standard position using the formula θ = arctan(b/a).
• Write the complex number in the form re^(jθ).

To convert from exponential form to rectangular form, we can use the following steps:

• Find the real part of the complex number using the formula a = rcos(θ).
• Find the imaginary part of the complex number using the formula b = rsin(θ).
• Write the complex number in the form a + bj.

Benefits of Converting Complex Numbers

Converting complex numbers to rectangular and exponential forms has several benefits, including:

• Simplifying calculations: Converting complex numbers to rectangular and exponential forms can simplify calculations, such as adding and subtracting complex numbers.
• Gaining insight: Converting complex numbers to rectangular and exponential forms can provide insight into the properties and behavior of complex numbers.
• Solving equations: Converting complex numbers to rectangular and exponential forms can be useful for solving equations, such as finding the roots of complex numbers.

Conclusion

Converting complex numbers to rectangular and exponential forms is an essential skill in mathematics and engineering. By understanding the rectangular and exponential forms of complex numbers, we can simplify calculations, gain insight into the properties and behavior of complex numbers, and solve equations. Whether you're working with complex numbers in your academic or professional pursuits, converting them to rectangular and exponential forms is a crucial step in unlocking their full potential.

We hope this article has helped you understand the importance of converting complex numbers to rectangular and exponential forms. Do you have any questions or comments about this topic? Please share them with us in the comments section below.