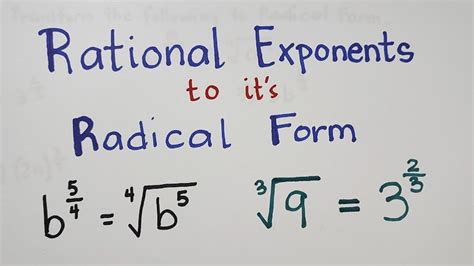Convert To Radical Form Made Easy

Quick Links :

Radical expressions can be intimidating, especially when it comes to converting them to radical form. However, with the right approach, it can be made easy. In this article, we will break down the steps to convert expressions to radical form, making it simple and straightforward.

Radical expressions are used to represent numbers that cannot be expressed as simple fractions. They are commonly used in mathematics, physics, and engineering. Converting expressions to radical form can help simplify complex calculations and provide a more intuitive understanding of mathematical concepts.

Understanding the Basics of Radical Expressions

Before we dive into converting expressions to radical form, let's review the basics. Radical expressions consist of a radical symbol (√), an index (which is optional), and a radicand (the number or expression inside the radical symbol). For example, √16 is a radical expression where 16 is the radicand.

Types of Radical Expressions

There are two types of radical expressions: square roots and nth roots. Square roots are the most common type and are denoted by the radical symbol (√) without an index. Nth roots are denoted by the radical symbol with an index (e.g., ∛, ∜).

Converting Expressions to Radical Form

Now that we have a basic understanding of radical expressions, let's move on to converting expressions to radical form. Here are the steps:

1. Identify the expression: Identify the expression you want to convert to radical form. It can be a fraction, a decimal, or an integer.
2. Determine the index: Determine the index of the radical expression. If the expression is a perfect square, the index is 2. If it's a perfect cube, the index is 3, and so on.
3. Find the radicand: Find the radicand by taking the expression and removing any perfect powers of the index. For example, if the expression is 16 and the index is 2, the radicand is 16.
4. Simplify the radicand: Simplify the radicand by factoring out any perfect powers of the index. For example, if the radicand is 16, it can be factored as 4^2.
5. Write the radical expression: Write the radical expression using the radical symbol, index (if necessary), and simplified radicand.

Examples of Converting Expressions to Radical Form

Here are some examples of converting expressions to radical form:

• Convert 16 to radical form: √16 = √(4^2) = 4
• Convert 27 to radical form: ∛27 = ∛(3^3) = 3
• Convert 64 to radical form: √64 = √(8^2) = 8

Common Mistakes to Avoid When Converting Expressions to Radical Form

When converting expressions to radical form, there are some common mistakes to avoid:

• Forgetting the index: Make sure to include the index (if necessary) when writing the radical expression.
• Not simplifying the radicand: Simplify the radicand by factoring out any perfect powers of the index.
• Not identifying perfect powers: Identify perfect powers of the index to simplify the radicand.

Practical Applications of Converting Expressions to Radical Form

Converting expressions to radical form has many practical applications in mathematics, physics, and engineering. Here are a few examples:

• Simplifying complex calculations: Converting expressions to radical form can simplify complex calculations and provide a more intuitive understanding of mathematical concepts.
• Solving equations: Converting expressions to radical form can help solve equations involving radicals.
• Analyzing data: Converting expressions to radical form can help analyze data in physics and engineering.

Conclusion

Converting expressions to radical form can be made easy by following the steps outlined in this article. By understanding the basics of radical expressions, identifying the expression, determining the index, finding the radicand, simplifying the radicand, and writing the radical expression, you can convert expressions to radical form with ease. Remember to avoid common mistakes and appreciate the practical applications of converting expressions to radical form.